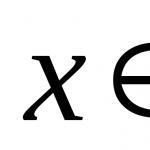Lidhja binare dhe karakteristikat e saj janë shembuj. Marrëdhëniet binare dhe vetitë e tyre

Produkt kartezian dy komplete X Dhe Y quajtur një grup të gjithë porositi çifte ( x, y ) sikurse
, A
.

Shembulli 1 . Le .

Pastaj, .

Është e qartë se
, d.m.th. produkti kartezian i veprimit të grupeve nuk është komutativ.

Produkt kartezian i grupeve
quajtur një grup
të gjitha kompletet e porositura
të tilla që nëse
, atëherë shënohet prodhimi kartezian
.

Do të themi se korrespondenca është dhënë q ndërmjet grupeve X Dhe Y, nëse jepet një treshe e porositur
, Ku
.Një tufë me X quhet zona e nisjes, dhe Y- zona e mbërritjes së korrespondencës q(shënoni
). Çdo element yçiftëzohet me
quhet imazhi i elementit x (x– prototipi i elementit y) për këtë korrespondencë q.

Korrespondencë
thirrur shfaqja grupe X ne shume Y, nëse çdo element
ka një imazh
, d.m.th.

Ekrani
thirrur funksionale , nëse çdo element
Ajo ka i vetmi imazh
:. Shumë imazhe për një ekran të caktuar
shënohet me
:.

Nëse grupi
përkon me grupin Y, atëherë ata thonë se
shfaq në një tufë me Y.

Korrespondencë
thirrur një me një (bijeksion) , nëse a) është një hartë; b) funksionalisht; c) shfaq X set "në". Y; d) nga gjendja
duhet
.

Me fjale te tjera,
është një bijeksion nëse çdo element
ka një imazh të vetëm
, dhe çdo element
ka një prototip të vetëm
me këtë ekran:

(1.2)

1.2.2 Përkufizimi i një relacioni binare

Përkufizimi. Ata thonë se në shumë X relacioni binare i dhënë R, nëse jepet një nëngrup i prodhimit kartezian
(ato.
).

Shembulli 2 . Le
Le ta vendosim atë në X marrëdhëniet e mëposhtme:

– raporti i barazisë;

– marrëdhënia e përparësisë;

i ndarë nga – relacioni i pjesëtueshmërisë.

Të gjitha këto marrëdhënie specifikohen duke përdorur një veti karakteristike. Elementet e kësaj marrëdhënieje janë renditur më poshtë:

Fakti që çifti ( x, y) i përket kësaj relacioni R, do të shkruajmë:
ose xRy. Për shembull, për lidhjen P hyrja 4 P 2 do të thotë 4 pjesëtohet me 2, d.m.th.

Domeni i përkufizimit
lidhje binare R quajtur një grup
Gama e vlerave
quajtur një grup

Po, për marrëdhënien R nga shembulli 2 domeni i përkufizimit është bashkësia
, dhe diapazoni i vlerave është
.

1.2.3 Metodat për përcaktimin e një relacioni binare

Një lidhje binare mund të specifikohet duke specifikuar një veçori karakteristike ose duke renditur të gjithë elementët e saj. Mënyrat më vizuale për të specifikuar një lidhje binare janë grafiku i relacionit, diagrami i marrëdhënieve, grafiku i relacioneve, matrica e relacioneve.

Orari marrëdhëniet përshkruhen në një sistem koordinativ kartezian; boshti horizontal shënon domenin e përkufizimit, boshti vertikal shënon grupin e vlerave të relacionit; elementi i lidhjes ( x, y) i përgjigjet një pike në rrafsh me këto koordinata. Në Fig. 1.7,a) tregon një grafik të raportit P shembulli 2.

Skema marrëdhëniet përshkruhen duke përdorur dy linja vertikale, e majta e të cilave korrespondon me domenin e përkufizimit të marrëdhënies, dhe e djathta me grupin e vlerave të marrëdhënies. Nëse elementi ( x, y) i përket relacionit R, pastaj pikat përkatëse nga
Dhe
të lidhura me një segment të drejtë. Në Fig. 1.7,b) tregon një diagram të marrëdhënies P nga shembulli 2.

Grafiku marrëdhënie
është ndërtuar si më poshtë. Pikat - elementet e grupit - përshkruhen në aeroplan në çdo mënyrë X. Çift pikësh X Dhe në lidhet me një hark (vijë me një shigjetë) nëse dhe vetëm nëse çifti ( x, y) i përket relacionit R. Në Fig. 1.8,a) tregon grafikun e relacionit P shembulli 2.

Le
. Matricë marrëdhënie
Ajo ka n linjat dhe n kolonat dhe elementi i saj përcaktohet nga rregulli:

Figura 1.8b) tregon matricën e relacionit P shembulli 2.

Përkufizime të ngjashme

Vetitë e marrëdhënieve

Marrëdhëniet binare mund të kenë veti të ndryshme, si p.sh

Llojet e marrëdhënieve

• Një relacion kalimtar refleksiv quhet relacion pothuajse i rendit.
• Një relacion kalimtar simetrik refleksiv quhet relacion ekuivalent.
• Një relacion kalimtar antisimetrik refleksiv quhet relacion i rendit (i pjesshëm).
• Një lidhje kalimtare anti-refleksive antisimetrike quhet një lidhje e rreptë e rendit.
• Një lidhje kalimtare e plotë antisimetrike (për çdo x, y xRy ose yRx) quhet relacion i rendit linear.
• Një marrëdhënie asimetrike antirefleksive quhet marrëdhënie dominimi.

Llojet e marrëdhënieve të dyfishta

• Qëndrim i kundërt [specifikoni] (lidhja e anasjelltë me R) është një lidhje binare e përbërë nga çifte elementësh (y, x) të përftuara nga ndërrimi i çifteve të elementeve (x, y) të një relacioni të caktuar R. Shënohet me: R −1. Për këtë relacion dhe inversin e saj është e vërtetë barazia e mëposhtme: (R −1) −1 = R.
• Marrëdhëniet reciproke(marrëdhënie reciproke) - marrëdhënie që janë të kundërta me njëra-tjetrën. Gama e vlerave të njërës prej tyre shërben si diapazoni i përcaktimit të tjetrit, dhe diapazoni i përcaktimit të të parit shërben si diapazoni i vlerave të tjetrit.
• Qëndrim reflektues- një lidhje binare R e përcaktuar në një bashkësi të caktuar dhe e karakterizuar në atë që për çdo x të kësaj bashkësie elementi x është në relacionin R me vetveten, domethënë për çdo element x të kësaj bashkësie vlen xRx. Shembuj të marrëdhënieve refleksive: barazi, njëkohshmëri, ngjashmëri.
• Qëndrim antireflektues(Një relacion jorefleksiv, vini re se ashtu si antisimetria nuk përkon me asimetrinë, jorefleksiviteti nuk përkon me jorefleksivitetin.) - një lidhje me dy vende R e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo element x të kësaj bashkësie ajo nuk është e vërtetë që është në relacionin R me vetveten (nuk është e vërtetë që xRx), domethënë është e mundur që një element i grupit të mos jetë në relacion R me vetveten. Shembuj të qëndrimeve jo reflektuese: "kujdes", "argëtojë", "nervoz".
• Lidhja kalimtare- një lidhje binare R, e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo x, y, z të këtij grupi, xRy dhe yRz nënkuptojnë xRz (xRy&yRzxRz). Shembuj të marrëdhënieve kalimtare: "më shumë", "më pak", "barabartë", "të ngjashme", "sipër", "veri".
• Lidhja jokalimtare [specifikoni] - një lidhje binare R e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo x, y, z të këtij grupi xRy dhe yRz nuk nënkuptojnë xRz ((xRy&yRzxRz)). Shembull i një relacioni jokalimtar: "x është babai i y"
• Lidhja simetrike- një lidhje me dy vende R, e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo element x dhe y të kësaj bashkësie, nga fakti që x është me y në relacion R (xRy), rrjedh se y është në të njëjtin lidhje me x ( yRx). Një shembull i marrëdhënieve simetrike mund të jetë barazia (=), marrëdhënia e ekuivalencës, ngjashmërisë, njëkohshmërisë, disa marrëdhënie farefisnore (për shembull, marrëdhënia e vëllazërisë).
• Lidhja antisimetrike- një lidhje me dy vende R, e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo x dhe y nga xRy dhe xR -1 y pason x = y (d.m.th., R dhe R -1 janë të kënaqur njëkohësisht vetëm për anëtarë të barabartë me njëri tjetrin).
• Marrëdhënie asimetrike [specifikoni] është një lidhje me dy vende R, e përcaktuar në një grup të caktuar dhe e karakterizuar në atë që për çdo x dhe y, xRy nënkupton yRx. Shembull: lidhja e "më shumë se" (>) dhe "më pak se" (<).
• Marrëdhënia e ekuivalencës(lidhja e identitetit [ specifikoni], relacioni i tipit të barazisë) është një lidhje me dy vende R ndërmjet objekteve x dhe y në fushën e temës D, që plotëson aksiomat (kushtet) e mëposhtme: Kështu, një relacion i llojit të barazisë është njëkohësisht refleksiv, simetrik dhe kalimtar. Shembuj: barazi, kardinalitet i barabartë i dy grupeve, shkëmbim mallrash në treg, ngjashmëri, njëkohësi. Një shembull i një lidhjeje që plotëson aksiomën (3), por nuk plotëson aksiomat (1) dhe (2): "më shumë".
• Rendit marrëdhëniet- marrëdhëniet që kanë vetëm disa nga tre vetitë e një relacioni ekuivalent. Në veçanti, një lidhje që është refleksive dhe kalimtare, por asimetrike (për shembull, "jo më") formon një rend "të dobët". Marrëdhënia është kalimtare, por jo-refleksive dhe asimetrike (për shembull, "më pak se") - një urdhër "i rreptë".
• Funksioni- lidhje e dyfishtë R, të përcaktuara në një grup të caktuar, të karakterizuar në atë për secilën vlerë x marrëdhënie xRy y. Shembull: " y babai x" Vetia e funksionalitetit të relacionit Rështë shkruar si një aksiomë: ( xRy Dhe xRz)→(y≡z). Meqenëse çdo vlerë x në shprehje xRy Dhe xRz korrespondon me të njëjtën vlerë, atëherë y Dhe z përkojnë, rezultojnë të jenë të njëjta. Lidhja funksionale është unike, pasi çdo vlerë x ka një relacion xRy korrespondon vetëm me një vlerë të vetme y, por jo anasjelltas.
• Bijeksion(relacion një vend) - relacion dyvendësh R, i përcaktuar në një grup të caktuar, i karakterizuar në atë që në të çdo vlerë x korrespondon me një vlerë të vetme në, dhe çdo vlerë në përputhet me një vlerë të vetme X. Një lidhje një-me-një është një rast i veçantë i një marrëdhënie një-me-një.
• Marrëdhënie e lidhur- kjo është një lidhje me dy vende R, i përcaktuar në një grup të caktuar, i karakterizuar në atë për çdo dy elementë të ndryshëm X Dhe në të këtij grupi, njëri prej tyre është në lidhje R tek tjetri (d.m.th., njëra nga dy marrëdhëniet është e kënaqur: xRy ose yRx). Shembull: relacioni "më pak se" (<).

Operacionet mbi marrëdhëniet

Meqenëse relacionet e përcaktuara në një çift të caktuar grupesh , , janë nënbashkësi të grupit , bashkësia e të gjitha këtyre marrëdhënieve formon një algjebër Bulean në lidhje me operacionet e bashkimit, kryqëzimit dhe shtimit të marrëdhënieve. Në veçanti, për arbitrare

Shpesh, në vend që të ndërthurin, kryqëzojnë dhe plotësojnë marrëdhëniet, ata flasin për ndarjen, lidhjen dhe mohimin e tyre.

Për shembull, , , domethënë, bashkimi i një relacioni të rendit të rreptë me një relacion barazie përkon me një relacion të rendit jo të rreptë, dhe kryqëzimi i tyre është bosh.

Përveç atyre të listuara, të rëndësishme janë edhe operacionet e përmbysjes dhe shumëzimit të marrëdhënieve, të përcaktuara si më poshtë.

Nëse , atëherë një lidhje e anasjelltë është një relacion i përcaktuar në çift dhe përbëhet nga ato çifte për të cilat . Për shembull, .

Le tani,. Produkti i marrëdhënieve është një lidhje e tillë që

Nëse , dhe , atëherë produkti i marrëdhënieve është i papërcaktuar. Nëse marrim parasysh marrëdhëniet e përcaktuara në një grup, atëherë një situatë e tillë nuk lind.

Për shembull, merrni parasysh një lidhje të rreptë të rendit të përcaktuar në grupin e numrave natyrorë. Është e lehtë të vërehet kjo

Marrëdhëniet binare quhen komutative nëse . Është e lehtë të shihet se për çdo lidhje binare të përcaktuar në , ku simboli tregon barazinë e përcaktuar në . Megjithatë, barazia nuk është gjithmonë e drejtë.

Identitetet e mëposhtme kanë:

Vini re se analogët e dy identiteteve të fundit nuk qëndrojnë.

Disa veti të një relacioni mund të përcaktohen duke përdorur operacionet e relacionit:

Shiko gjithashtu

Letërsia

• A. I. Maltsev. Sistemet algjebrike. - M.: Shkencë, 1970.

Fondacioni Wikimedia. 2010.

- një kallëzues dyvendësh në një bashkësi të caktuar. Nën B. o. ndonjëherë kuptohet si një nëngrup i grupit të çifteve të renditura (a, 6) të elementeve të një grupi të caktuar A. B. o. një rast i veçantë i një marrëdhënieje. Le te jete. Nëse, atëherë thuhet se elementi është në binar... ... Enciklopedia Matematikore

Në logjikë, diçka që, ndryshe nga një veti, karakterizon jo një objekt individual, por një çift, tre, etj. artikujt. Logjika tradicionale nuk e konsideronte O.; në logjikën moderne O. është një funksion propozicional i dy ose më shumë ndryshoreve. Binar... Enciklopedi Filozofike

qëndrim- MARRËDHËNIET është një grup individësh n ok të renditur (ku n është 1), d.m.th. dyshe, treshe etj. Numri n quhet "lokalitet", ose "aritet", O. dhe, në përputhje me rrethanat, ata flasin për n lokal (n arno) O. Kështu, për shembull, një O. e dyfishtë quhet... ... Enciklopedia e Epistemologjisë dhe Filozofisë së Shkencës

Në teorinë e konsumatorit, ky është një përshkrim formal i aftësisë së konsumatorit për të krahasuar (renditur sipas dëshirës) grupe të ndryshme të mallrave (paketat e konsumit). Për të përshkruar një marrëdhënie preference, nuk është e nevojshme të matet dëshirueshmëria... ... Wikipedia

Ky term ka kuptime të tjera, shih Qëndrimi. Një lidhje është një strukturë matematikore që përcakton zyrtarisht vetitë e objekteve të ndryshme dhe marrëdhëniet e tyre. Marrëdhëniet zakonisht klasifikohen sipas numrit të objekteve që lidhen... Wikipedia

Ky term ka kuptime të tjera, shih Qëndrimi. Një lidhje në logjikën e rendit të parë me dy ose më shumë kallëzues argumentesh (kallëzues të shumëfishtë), dy ose më shumë veti kallëzuese. Shenja e marrëdhënies: R.[specifiko] Për sa i përket marrëdhënieve... ... Wikipedia, A.I. Shirokov. Manuali është pjesa e shtatë e rubrikës “Ndërtimet bazë teorike të bashkësive” të disiplinës akademike “Matematika diskrete”. Ai prezanton dhe analizon të tilla... ebook

Le Rështë një lidhje binare në bashkësinë X, dhe x, y, z janë ndonjë nga elementët e tij. Nëse një element x është në një marrëdhënie R me një element y, atëherë shkruani xRy.

1. Një relacion R në një bashkësi X quhet refleksiv nëse çdo element i grupit është në këtë lidhje me vetveten.

R-refleksiv në X<=>xRx për çdo x€ X

Nëse relacioni R është refleksiv, atëherë ka një lak në çdo kulm të grafikut. Për shembull, marrëdhëniet e barazisë dhe paralelizmit për segmentet janë refleksive, por marrëdhëniet e pingulitetit dhe "më të gjata" nuk janë refleksive. Kjo pasqyrohet në grafikët në Figurën 42.

2. Një lidhje R në një bashkësi X quhet simetrike nëse nga fakti se elementi x është në një marrëdhënie të caktuar me elementin y, rezulton se elementi y është në të njëjtën marrëdhënie me elementin x.

R - në mënyrë simetrike (xYay =>y Rx)

Një grafik relacioni simetrik përmban shigjeta të çiftëzuara që shkojnë në drejtime të kundërta. Marrëdhëniet e paralelizmit, pingulitetit dhe barazisë për segmentet janë simetrike, por relacioni “më i gjatë” nuk është simetrik (Fig. 42).

3. Një lidhje R në një bashkësi X quhet antisimetrik nëse, për elementë të ndryshëm x dhe y nga bashkësia X, nga fakti se elementi x është në një lidhje të caktuar me elementin y, rezulton se elementi y nuk është në këtë lidhje me elementin x.

R - antisimetrik në X « (xRy dhe xy ≠ yRx)

Shënim: një mbibar tregon mohimin e një deklarate.

Në një grafik relacioni antisimetrik, dy pika mund të lidhen vetëm me një shigjetë. Një shembull i një lidhjeje të tillë është relacioni “më i gjatë” për segmentet (Fig. 42). Marrëdhëniet e paralelizmit, pingulitetit dhe barazisë nuk janë antisimetrike. Ka marrëdhënie që nuk janë as simetrike dhe as antisimetrike, për shembull relacioni “të jesh vëlla” (Fig. 40).

4. Një lidhje R në një bashkësi X quhet kalimtare nëse nga fakti se një element x është në një lidhje të caktuar me një element y dhe një element y është në këtë relacion me një element z, rezulton se elementi x është në një lidhje e dhënë me një element Z

R - kalimtare në A≠ (xRy dhe yRz=> xRz)

Në grafikët e marrëdhënieve "më të gjata", paralelizmi dhe barazie në figurën 42, mund të vini re se nëse një shigjetë shkon nga elementi i parë në të dytin dhe nga i dyti në të tretën, atëherë patjetër që ka një shigjetë që shkon nga i pari. element në të tretën. Këto marrëdhënie janë kalimtare. Perpendikulariteti i segmenteve nuk ka vetinë e kalueshmërisë.

Ekzistojnë veti të tjera të marrëdhënieve midis elementeve të së njëjtës bashkësi që ne nuk i konsiderojmë.

E njëjta lidhje mund të ketë disa veti. Kështu, për shembull, në një grup segmentesh, marrëdhënia "e barabartë" është refleksive, simetrike, kalimtare; relacioni “më shumë” është antisimetrik dhe kalimtar.

Nëse një lidhje në një bashkësi X është refleksive, simetrike dhe kalimtare, atëherë ajo është një lidhje ekuivalente në këtë grup. Marrëdhënie të tilla e ndajnë bashkësinë X në klasa.

Këto marrëdhënie manifestohen, për shembull, kur plotësoni detyrat: "Merrni shirita me gjatësi të barabartë dhe rregulloni ato në grupe", "Rregulloni topat në mënyrë që secila kuti të përmbajë topa me të njëjtën ngjyrë". Marrëdhëniet e ekuivalencës (“të jenë të barabarta në gjatësi”, “të jenë të së njëjtës ngjyrë”) përcaktojnë në këtë rast ndarjen e grupeve të shiritave dhe topave në klasa.

Nëse një lidhje në grupin 1 është kalimtare dhe antisimetrike, atëherë ajo quhet relacion i rendit në këtë grup.

Një bashkësi me një relacion të caktuar të rendit quhet bashkësi e renditur.

Për shembull, kur kryeni detyrat: "Krahasoni shiritat në gjerësi dhe rregulloni ato nga më e ngushta tek më e gjera", "Krahasoni numrat dhe rregulloni kartat e numrave sipas radhës", fëmijët renditin elementet e grupeve të shiritave dhe kartave të numrave. duke përdorur marrëdhëniet e rendit; "të jesh më i gjerë", "të ndjekësh".

Në përgjithësi, marrëdhëniet e ekuivalencës dhe rendit luajnë një rol të madh në formimin tek fëmijët e ideve të sakta për klasifikimin dhe renditjen e grupeve. Përveç kësaj, ka shumë marrëdhënie të tjera që nuk janë as marrëdhënie ekuivalente dhe as marrëdhënie të rendit.

6. Cila është vetia karakteristike e një bashkësie?

7. Në çfarë marrëdhëniesh mund të ekzistojnë bashkësitë? Jepni shpjegime për çdo rast dhe përshkruani ato duke përdorur rrathët e Euler-it.

8. Përcaktoni një nëngrup. Jepni një shembull të grupeve, njëra prej të cilave është një nëngrup i një tjetri. Shkruani marrëdhëniet e tyre duke përdorur simbole.

9. Përcaktoni grupe të barabarta. Jepni shembuj të dy grupeve të barabarta. Shkruani marrëdhëniet e tyre duke përdorur simbole.

10. Përcaktoni kryqëzimin e dy grupeve dhe përshkruani atë duke përdorur rrathët e Euler-it për çdo rast të veçantë.

11. Përcaktoni bashkimin e dy grupeve dhe përshkruani atë duke përdorur rrathët e Euler-it për çdo rast të veçantë.

12. Përcaktoni ndryshimin midis dy grupeve dhe përshkruani atë duke përdorur rrathët e Euler-it për çdo rast të veçantë.

13. Përcaktoni komplementin dhe përshkruani atë duke përdorur rrathët e Euler-it.

14. Çfarë quhet ndarja e një grupi në klasa? Emërtoni kushtet për klasifikimin e saktë.

15. Çfarë quhet korrespodencë ndërmjet dy grupeve? Emërtoni metodat për specifikimin e korrespondencave.

16. Çfarë lloj korrespondence quhet një me një?

17. Cilat bashkësi quhen të barabarta?

18. Cilat bashkësi quhen ekuivalente?

19. Emërtoni mënyra për të përcaktuar marrëdhëniet në një grup.

20. Cila lidhje në një bashkësi quhet refleksive?

21. Cila lidhje në një bashkësi quhet simetrike?

22. Cila lidhje në një bashkësi quhet antisimetrike?

23. Cila lidhje në një bashkësi quhet kalimtare?

24. Përcaktoni një lidhje ekuivalente.

25. Përcaktoni relacionin e rendit.

26. Cili grup quhet i renditur?

Gjuha T-SQL në SQL Server bazohet në gjuhën standarde SQL, e cila bazohet në modelin relacional, i cili nga ana tjetër bazohet në baza matematikore si teoria e grupeve dhe logjika e kallëzuesit. Ky artikull shqyrton një temë themelore nga teoria e grupeve: vetitë e marrëdhënieve në grupe. Lexuesit mund të përdorin kodet e propozuara T-SQL për të kontrolluar praninë e veçorive të caktuara të marrëdhënieve të caktuara. Megjithatë, mund të provoni gjithashtu të shkruani versionet tuaja të skripteve (për të përcaktuar nëse një lidhje ka një veti të veçantë) përpara se të aplikoni zgjidhjet e përshkruara në këtë artikull.

Komplete dhe marrëdhënie

Georg Cantor, krijuesi i teorisë së grupeve, e përkufizon një grup si "bashkim në një tërësi të caktuar M të një koleksioni objektesh të caktuara qartësisht të dallueshme m të soditjes ose mendimit tonë (të cilat do të quhen elementë të grupit M). Elementet e një grupi mund të jenë objekte të natyrës arbitrare: njerëzit, numrat, madje edhe vetë grupet. Simbolet ∈ dhe ∉ tregojnë, respektivisht, operatorët që pasqyrojnë anëtarësimin (ndodhjen, anëtarësimin) dhe mosanëtarësimin e një elementi në një grup. Kështu, shënimi x ∈ V do të thotë se x është një element i grupit V, dhe shënimi x ∉ V do të thotë se x nuk është një element i V.

Një lidhje binare në një grup është një grup çiftesh të renditura elementësh të grupit origjinal. Kështu, për një grup elementësh V = (a, b, c), një lidhje binare R në një bashkësi të caktuar V do të jetë një nëngrup arbitrar i bashkësisë së të gjitha çifteve të renditura të produktit kartezian V × V = ((a, a), (a, b), (a , c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c) ). Marrëdhënia R = ((a, b), (b, c), (a, c)) është një lidhje binare e vlefshme në V. Mund të themi se a është e lidhur me b nga R. Supozojmë se R = ((a , b ), (b, c), (c, d)). Një R e tillë nuk është një lidhje e pranueshme në V, pasi çifti (c, d) nuk i përket produktit kartezian V × V. Vini re se rendi në të cilin janë specifikuar elementët e përfshirë në grup nuk është i rëndësishëm. Bashkësia V mund të specifikohet si (a, b, c) ose si (b, a, c) dhe kështu me radhë. Megjithatë, renditja në çiftet e renditura, si (a, b) e një relacioni binare, është e rëndësishme; kështu (a, b) ≠ (b, a).

Si një shembull më realist i një lidhjeje binare, merrni parasysh grupin F të anëtarëve të familjes: (Itsik, Mickey, Inna, Mila, Gabi). Mickey është vëllai binjak i Itzik, Inna është motra e tij e madhe, Mila është nëna e tij dhe Gabi është babai i tij. Një shembull i një lidhjeje R në një grup F do të ishte: "është një vëlla". Elementet e kësaj marrëdhënieje janë ((Itsik, Mickey), (Mickey, Itzik), (Itsik, Inna), (Mickey, Inna)). Vëmë re se çifti i renditur (Itsik, Inna) shfaqet në R, por çifti (Inna, Itsik) jo. Edhe pse Itzik është vëllai i Inës, ajo nuk është vëllai i tij.

Vetitë e marrëdhënieve në grupe

Tani që kemi rifreskuar të kuptuarit tonë për grupet dhe marrëdhëniet, le të kalojmë në temën e artikullit - vetitë e marrëdhënieve në grupe. Për shembull të dhëna, përdorni kodin në Listimin 1 për të krijuar tabela V dhe R. V do të përfaqësojë një grup, dhe R do të përfaqësojë një lidhje binare në të. Përdorni kodin në Listimin 2 për të krijuar një procedurë ClearTables që do t'i pastrojë të dyja këto tabela të të dhënave përpara se t'i plotësojë ato me të dhëna të reja mostër. Së fundi, përdorni kodin në Listimet 3, 4 dhe 5 për të mbushur tabelat V dhe R me grupe të ndryshme të dhënash për testim (ne do t'i quajmë ato të dhëna të mostrës 1, 2 dhe 3, respektivisht).

Refleksiviteti. Një relacion R në një bashkësi V është refleksiv nëse për çdo element v të bashkësisë V, v ∈ V, rrjedh se (v, v) ∈ R, domethënë çifti (v, v) i përket gjithmonë R. Dhe relacioni R në V nuk është refleksiv, nëse ekziston një element v ∈ V i tillë që çifti (v, v) ∉ R. Shqyrtoni përsëri shembullin e bashkësisë F - anëtarët e familjes sime.

Lidhja "të jesh në të njëjtën moshë si" në F është padyshim refleksive. Elementet e marrëdhënies do të jenë çiftet e mëposhtme: ((Itsik, Itsik), (Itsik, Mickey), (Mickey, Mickey), (Mickey, Itzik), (Inna, Inna), (Mila, Mila), (Gabi , Gabi)).

Le të fillojmë të shkruajmë një pyetje T-SQL kundër tabelave V dhe R (që përfaqëson një grup dhe një lidhje në këtë grup), duke kontrolluar nëse R është refleksiv:

ZGJIDH
RAST
KUR EKZISTON
(SELECT v, v NGA dbo.V
PËRVEÇ
ZGJIDH r1, r2 NGA dbo.R)
PASTAJ "Jo"
TJETER "Po"
FUND SI refleksiv

Nënpyetja e parë në operacionin EXCEPT kthen grupin e të gjitha çifteve të renditura (v, v) për të gjitha rreshtat e tabelës V. Nënpyetja e dytë kthen grupin e çifteve të renditura (r1, r2) - të gjitha rreshtat e tabelës R. Operacioni EXCEPT do të kthejë kështu të gjitha çiftet e renditura që ndodhin në të parën dhe që mungojnë në setin e dytë. Kallëzuesi EXISTS nevojitet për të kontrolluar ekzistencën e të paktën një rekord në grupin e rezultateve. Nëse ka të paktën një regjistrim të tillë, atëherë shprehja CASE do të kthejë "Jo" (pa refleksivitet), por edhe "Po" përndryshe (ka refleksivitet).

Hidhini një sy tre grupeve të të dhënave të shembujve në Listimet 3, 4 dhe 5 dhe përpiquni të përcaktoni se cilat prej tyre do të kishin një marrëdhënie reflektuese pa kryer një pyetje. Përgjigjet janë dhënë më tej në tekstin e artikullit.

I pareflektues. Një relacion R në një grup V quhet jorefleksiv (të mos ngatërrohet me jorefleksivitetin) nëse për çdo element v ∈ V rezulton se (v, v) ∉ R. Një relacion nuk është jorefleksiv nëse ka një element v ∈ V për të cilën (v, v) ∈ R. Një shembull i një lidhjeje jorefleksive në bashkësinë F të anëtarëve të familjes sime është relacioni “të jesh prind”, pasi asnjë person nuk mund të jetë prindi i tij. Anëtarët e kësaj lidhjeje në F do të jenë dyshet e mëposhtme: ((Mila, Itzik), (Mila, Mickey), (Mila, Inna), (Gabi, Itzik), (Gabi, Mickey), (Gabi, Inna)) .

Pyetja e mëposhtme kontrollon nëse relacioni R në V është jorefleksiv:

ZGJIDH
RAST
KUR EKZISTON
(ZGJIDH * NGA dbo.R
KU r1 = r2)
PASTAJ "Jo"
TJETER "Po"
FUND SI irrefleksiv

Çelësat e huaj në përkufizimin e tabelës R u prezantuan për të siguruar që vetëm elementët e V mund të përbëjnë atributet r1 dhe r2 të një rekord R. Kështu, gjithçka që mbetet është të kontrollohet nëse ka regjistrime në R me atribute që përputhen r1 dhe r2. Nëse gjendet një hyrje e tillë, relacioni R nuk është jorefleksiv; nëse nuk ka hyrje, ai është jorefleksiv.

Simetria. Një relacion R në një grup V quhet simetrik nëse, së bashku me (r1, r2) ∈ R, (r2, r1) ∈ R është gjithmonë i kënaqur. Lidhja nuk është simetrike nëse ka një çift (r1, r2) ∈ R për të cilat (r2, r1) ∉ R. Në bashkësinë F të anëtarëve të familjes Ben-Gan, relacioni "është një vëlla i" do të ishte shembull i një lidhjeje simetrike. Dyshet e kësaj relacioni do të jenë grupet e mëposhtme: ((Itsik, Mickey), (Itsik, Inna), (Mickey, Itzik), (Mickey, Inna), (Inna, Itzik), (Inna, Mickey)).

Pyetja e mëposhtme kontrollon nëse lidhja R me V është simetrike:

ZGJIDH
RAST
KUR EKZISTON
(ZGJIDHni r1, r2 NGA dbo.R
PËRVEÇ
ZGJIDH r2, r1 NGA dbo.R)
PASTAJ "Jo"
TJETER "Po"
FUNDIT SI simetrik

Kodi i kërkesës përdor operacionin EXCEPT. Nënpyetja e parë e operacionit EXCEPT kthen një grup çiftesh të renditura (r1, r2) - regjistrime të tabelës R, dhe e dyta - një grup çiftesh të renditura (r2, r1) për çdo rekord të R. Nëse relacioni R në grupi V nuk është simetrik, atëherë operacioni EXCEPT do të kthejë një grup rezultatesh jo bosh, dhe kallëzuesi EXISTS, respektivisht, vlerën TRUE dhe, së fundi, shprehja CASE do të kthejë "Jo".

Nëse marrëdhënia është simetrike, atëherë shprehja CASE do të japë "Po".

Asimetria. Një lidhje R në një bashkësi V është asimetrike (kjo veti nuk duhet të ngatërrohet me asimetrinë) nëse për çdo bashkësi (r1, r2) ∈ R, në të cilën r1 ≠ r2, është e vërtetë që (r2, r1) ∉ R. An shembull i një lidhjeje asimetrike në një grup F anëtarët e familjes së autorit do të kenë marrëdhënien "të jesh prind" që u përshkrua më sipër. Si ushtrim, përpiquni të gjeni një shembull të një lidhjeje në një grup jo bosh që është simetrik dhe asimetrik. Shikoni të dhënat e shembullit në këtë artikull për një zgjidhje.

ZGJIDH
RAST
KUR EKZISTON
(ZGJEDHni r1, r2 NGA dbo.R KU r1 r2
KRYQËZOHET
ZGJEDH r2, r1 NGA dbo.R WHERE r1 r2)
PASTAJ "Jo"
TJETER "Po"
FUNDIT SI asimetrik

Kodi përdor operacionin INTERSECT. Nënpyetja e parë në këtë operacion kthen çiftin e renditur (r1, r2) për çdo rekord të tabelës R në të cilën r1 r2.

Nënpyetja e dytë e operacionit INTERSECT kthen çiftin e renditur (r2, r1) për çdo regjistrim të tabelës R në të cilën r1 r2. Nëse grupi i rezultateve (rezultati i kryqëzimit të këtyre grupeve) përfshin të paktën një rekord, kjo do të thotë se R nuk është asimetrik; përndryshe R është asimetrike.

Transitiviteti. Një lidhje R në një grup V është kalimtare nëse përfshirjet (a, b) ∈ R dhe (b, c) ∈ R gjithmonë nënkuptojnë se (a, c) ∈ R. Një shembull i një lidhjeje kalimtare në një grup anëtarësh të familjes F do të ishte marrëdhënia "është vëlla apo motër" e cila u diskutua më lart.

Kodi më poshtë teston transitivitetin e relacionit R:

ZGJIDH
RAST
KUR EKZISTON
(ZGJIDH *
NGA dbo.R AS RA
BASHKIMI I BRENDSHËM dbo.R AS RB
NË RA.r2 = RB.r1
LEFT JASHT BASHKIM dbo.R AS RC
NË RA.r1 = RC.r1 DHE RB.r2 = RC.r2
KU RC.r1 ËSHTË NULL)
PASTAJ "Jo"
TJETER "Po"
FUND SI kalimtar

Kodi fillimisht përdor një bashkim të brendshëm midis dy instancave të R për të zgjedhur vetëm ato rreshta ku r2 në shkallën e parë përputhet me r1 në shkallën e dytë. Së dyti, kodi përdor një bashkim të jashtëm të majtë me shembullin e tretë të tabelës R, sipas të cilit r1 i shkallës së parë të R është i njëjtë me r1 i shkallës së tretë dhe r2 i shkallës së dytë është i njëjtë me r2 të shkallës së tretë. e treta. Nëse ka të paktën një rresht rezultati në nënpyetësin e brendshëm (kushti i përzgjedhjes për instancën e tretë: r1 është Null), kjo do të thotë se relacioni nuk është kalimtar; përndryshe relacioni R është kalimtar.

Marrëdhënie ekuivalente. Një relacion ekuivalent është një relacion që ka njëkohësisht vetitë e refleksivitetit, simetrisë dhe kalueshmërisë. Ju mund të përdorni pyetjet e sugjeruara më sipër për të kontrolluar veçmas për praninë e secilës veti: nëse një relacion i ka të treja, atëherë duhet të konkludojmë se ekziston një lidhje ekuivalente. Për më tepër, mund të përdorni kodin në Listën 6 për të testuar të gjitha vetitë e një relacioni R në një grup V që u diskutuan më herët në artikull, duke përfshirë testimin e vetive të të qenit një lidhje ekuivalente. Nëse ekzekutoni Listimin 6 në të dhënat e mostrës 1, 2 dhe 3 (të rrjedhura nga Listimet 3, 4 dhe 5, respektivisht), do të merrni rezultatet e treguara në Tabelat 1, 2 dhe 3, respektivisht.

Kthimi në bazat T-SQL

Kështu, ne kemi shqyrtuar një temë themelore nga teoria matematikore e bashkësive: vetitë e marrëdhënieve në bashkësi. Unë kam propozuar kode testimi T-SQL për të testuar vetitë e disa relacioneve të përfaqësuara nga tabela R (çiftet e renditura të elementeve) në grupin e elementeve të paraqitur nga tabela V.

Përdorimi i konstrukteve bazë T-SQL na ndihmoi të konfiguronim dhe zbatonim saktë veglat e kësaj gjuhe për një kuptim më të mirë të vetive të marrëdhënieve në grupe.

Itzik Ben-Gan ( [email i mbrojtur]) - mësues dhe konsulent, autor i librave mbi T-SQL, ka titullin SQL Server MVP

Leksioni 3.

klauzola 3. Marrëdhëniet në grupe. Vetitë e marrëdhënieve binare.

3.1. Marrëdhëniet binare.

Kur flasin për marrëdhëniet e dy njerëzve, për shembull, Sergei dhe Anna, ata nënkuptojnë se ka një familje të caktuar të cilës i përkasin. Një çift i renditur (Sergei, Anna) ndryshon nga çiftet e tjera të renditura të njerëzve në atë që ekziston një lloj marrëdhënieje midis Sergeit dhe Anna (kushëriri, babai, etj.).

Në matematikë, midis të gjitha çifteve të renditura të produktit të drejtpërdrejtë të dy grupeve A Dhe B (A´ B) çiftet “të veçanta” dallohen edhe për faktin se ndërmjet përbërësve të tyre ka disa marrëdhënie “farefisnore” që të tjerët nuk i kanë. Si shembull, merrni parasysh grupin S studentë të disa universiteteve dhe shumë K kurse që mësohen atje. Në një produkt të drejtpërdrejtë S´ K mund të zgjidhni një nëngrup të madh çiftesh të renditura ( s, k) që ka pasurinë: student sështë duke marrë një kurs k. Nëngrupi i ndërtuar pasqyron marrëdhënien "...dëgjon..." që lind natyrshëm midis grupeve të studentëve dhe kurseve.

Për një përshkrim të rreptë matematikor të çdo lidhjeje midis elementeve të dy grupeve, ne prezantojmë konceptin e një relacioni binare.

Përkufizimi 3.1. Binar (ose dyfishtë )qëndrim r ndërmjet grupeve A Dhe B quhet një nënbashkësi arbitrare A´ B, d.m.th.

Në veçanti, nëse A=B(d.m.th. rÍ A 2), atëherë ata thonë se r është një relacion në grup A.

Elementet a Dhe b quhen komponentët (ose koordinatat ) marrëdhënie r.

Koment. Le të biem dakord që për të treguar marrëdhëniet midis elementeve të grupeve, përdorni alfabetin grek: r, t, j, s, w, etj.

Përkufizimi 3.2. Domeni i përkufizimit D r=( a| $ b, Çfarë a r b) (ana e majte). Gama e vlerave e një relacioni binare r quhet bashkësi R r=( b| $ a, Çfarë a r b) (pjesa e djathtë).

Shembull 3. 1. Le të jepen dy grupe A=(1; 3; 5; 7) dhe B=(2; 4; 6). Le ta vendosim relacionin si më poshtë t=(( x; y)Î A´ B | x+y= 9). Kjo lidhje do të përbëhet nga çiftet e mëposhtme (3; 6), (5; 4) dhe (7; 2), të cilat mund të shkruhen si t=((3; 6), (5; 4), (7;2). ) ). Në këtë shembull D t=(3; 5; 7) dhe R t= B={2; 4; 6}.

Shembull 3. 2. Lidhja e barazisë në bashkësinë e numrave realë është bashkësia r=(( x; y) | x Dhe y– numra realë dhe x barazohet y). Ekziston një shënim i veçantë për këtë marrëdhënie: "=". Fusha e përkufizimit përkon me domenin e vlerave dhe është bashkësia e numrave realë, D r= R r.

Shembull 3. 3. Le A– shumë mallra në dyqan, dhe B– grup numrash realë. Pastaj j=(( x; y)Î A´ B | y– çmimi x) – lidhje bashkësive A Dhe B.

Nëse i kushtoni vëmendje shembullit 3.1., do të vini re se kjo lidhje është specifikuar fillimisht në formën t=(( x; y)Î A´ B | x+y=9), dhe më pas shkruhet si t=((3; 6), (5;4), (7;2)). Kjo sugjeron që marrëdhëniet në grupe (ose një grup) mund të specifikohen në mënyra të ndryshme. Le të shohim mënyrat për të përcaktuar marrëdhëniet binare.

Metodat për përcaktimin e marrëdhënieve:

1) duke përdorur një kallëzues të përshtatshëm;

2) një grup çiftesh të renditura;

3) në formë grafike: le A Dhe B– dy bashkësi të fundme dhe r – një lidhje binare ndërmjet tyre. Elementet e këtyre grupeve përfaqësohen me pika në rrafsh. Për çdo çift të renditur marrëdhëniesh, r vizaton një shigjetë që lidh pikat që përfaqësojnë përbërësit e çiftit. Një objekt i tillë quhet grafiku i drejtuar ose digrafi, zakonisht quhen pikat që përfaqësojnë elementet e bashkësive kulmet e grafikut.

4) në formën e një matrice: le A={a 1, a 2, …, një) Dhe B={b 1, b 2, …, bm), r – raporti aktiv A´ B. Paraqitja e matricës r quhet matricë M=[mij] madhësia n´ m, të përcaktuara nga marrëdhëniet

.

Nga rruga, përfaqësimi i matricës është një paraqitje e një relacioni në një kompjuter.

Shembull 3. 4. Le të jepen dy grupe A=(1; 3; 5; 7) dhe B=(2; 4; 6). Lidhja jepet si më poshtë t=(( x; y) | x+y= 9). Përcaktoni këtë lidhje si një grup çiftesh të renditura, një digraf, në formën e një matrice.

Zgjidhje. 1) t=((3; 6), (5; 4), (7; 2)) - është një përkufizim i një relacioni si një grup çiftesh të renditura;

2) grafiku përkatës i drejtuar është paraqitur në figurë.

https://pandia.ru/text/78/250/images/image004_92.gif" width="125" height="117">. ,

Shembull 3. 5 . Si shembull, ne mund të konsiderojmë të propozuar J. von Neumann(1903 – 1957) bllok diagrami i një kompjuteri sekuencial, i cili përbëhet nga shumë pajisje M:

,

Ku a- pajisje hyrëse, b- pajisje aritmetike (procesor), c- pajisje kontrolli, d- Pajisja e memories, e– pajisje dalëse.

Le të shqyrtojmë shkëmbimin e informacionit midis pajisjeve mi Dhe mj, të cilat janë në relacion r nëse nga pajisja mi informacioni hyn në pajisje mj.

Kjo lidhje binare mund të përcaktohet duke renditur të gjitha 14 çiftet e renditura të elementeve të saj:

Digrafi përkatës që përcakton këtë lidhje binare është paraqitur në figurë:

Paraqitja matricore e kësaj relacioni binare është:

. ,

Për marrëdhëniet binare, operacionet teorike të grupeve përcaktohen në mënyrën e zakonshme: bashkimi, kryqëzimi, etj.

Le të prezantojmë një koncept të përgjithësuar të marrëdhënies.

Përkufizimi 3.3. n-vend (n-ari ) relacioni r është një nëngrup i produktit të drejtpërdrejtë n grupe, domethënë një grup grupesh të renditura ( tuples )

rÍ A 1 Një={(a 1, …, një)| a 1О A 1Ù…Ù njëÎ Një}

Është i përshtatshëm për të përcaktuar marrëdhëniet me shumë vende duke përdorur tabela relacionale . Kjo detyrë korrespondon me numërimin e grupit n-me lidhjen r. Tabelat relacionale përdoren gjerësisht në praktikën kompjuterike në bazat e të dhënave relacionale. Vini re se tabelat relacionale përdoren në praktikën e përditshme. Të gjitha llojet e raporteve prodhuese, financiare, shkencore dhe të tjera shpesh marrin formën e tabelave relacionale.

fjala " relacionale" vjen nga fjala latine lidhje, që përkthehet në rusisht do të thotë "qëndrim". Prandaj, në literaturë, shkronja përdoret për të treguar marrëdhënien R(latinisht) ose r (greqisht).

Përkufizimi 3.4. Le të rÍ A´ B ka një qëndrim ndaj A´ B. Atëherë thirret raporti r-1 lidhje e anasjelltë me një raport të caktuar r nga A´ B, i cili përcaktohet si më poshtë:

r-1=(( b, a) | (a, b)Îr).

Përkufizimi 3.5. Le të r Н A´ B ka një qëndrim ndaj A´ B, a s Н B´ C - qëndrimi ndaj B´ C. Përbërja marrëdhëniet s dhe r quhet relacioni t Н A´ C, e cila përcaktohet si më poshtë:

t=s◦r= (( a, c)| $bÎ B, çfarë (a, b)Îr Dhe (b, c) Is).

Shembull 3. 6 . Le dhe C=(, !, d, a). Dhe le të jetë raporti r A´ B dhe raporti është i ndezur B´ C jepen në formën:

r=((1, x), (1, y), (3, x)};

s=(( x,), (x, !), (y, d), ( y, à)}.

Gjeni r-1 dhe s◦r, r◦s.

Zgjidhje. 1) Sipas përkufizimit r-1=(( x, 1), (y, 1), (x, 3)};

2) Duke përdorur përkufizimin e përbërjes së dy marrëdhënieve, marrim

s◦r=((1,), (1, !), (1, d), (1, а), (3,), (3, !)),

që nga (1, x)Ir dhe ( x,)Îs vijon (1,)Îs◦r;

nga (1, x)Ir dhe ( x, !)Îs vijon (1, !)Îs◦r;

nga (1, y)Ir dhe ( y, d)Îs vijon (1, d)Îs◦r;

nga (3, x)Ir dhe ( x, !)Îs vijon (3, !)Îs◦r.

Teorema 3.1. Për çdo marrëdhënie binare mbahen vetitë e mëposhtme:

2) ;

3) - asociativiteti i përbërjes.

Dëshmi. Vetia 1 është e dukshme.

Le të vërtetojmë vetinë 2. Për të vërtetuar vetinë e dytë, do të tregojmë se bashkësitë e shkruara në anën e majtë dhe të djathtë të barazisë përbëhen nga të njëjtat elementë. le ( a; b) О (s◦r)-1 Û ( b; a) О s◦r Û $ c sikurse ( b; c) О r dhe ( c; a) О s Û $ c sikurse ( c; b) О r-1 dhe ( a; c) О s-1 Ш ( a; b) О r -1◦s -1.

Vërtetoni vetë pronësinë 3.

3.2. Vetitë e marrëdhënieve binare.

Le të shqyrtojmë vetitë e veçanta të marrëdhënieve binare në grup A.

Vetitë e marrëdhënieve binare.

1. Raporti r në A´ A thirrur reflektuese , nese ( a,a) i përket r për të gjithë a nga A.

2. Relacioni r quhet antireflektues , nese nga ( a,b)Îr ndjek a¹ b.

3. Raporti r në mënyrë simetrike , nëse për a Dhe b i perket A, nga ( a,b) Nga kjo rrjedh se ( b,a)Îr.

4. Relacioni r quhet antisimetrike , nëse për a Dhe b nga A, nga përkatësia ( a,b) Dhe ( b,a) relacioni r nënkupton atë a=b.

5. Raporti r në mënyrë kalimtare , nëse për a, b Dhe c nga A nga fakti se ( a,b)Ir dhe ( b,c)Ir, rrjedh se ( a,c)Îr.

Shembull 3. 7. Le A=(1; 2; 3; 4; 5; 6). Në këtë bashkësi jepet relacioni rÍ A 2, e cila ka formën: r=((1, 1), (2, 2), (3, 3), (4; 4), (5; 5), (6; 6), (1; 2 ) , (1; 4), (2; 1), (2;4), (3;5), (5; 3), (4; 1), (4; 2)). Çfarë karakteristikash ka kjo marrëdhënie?

Zgjidhje. 1) Kjo marrëdhënie është refleksive, pasi për secilën aÎ A, (a; a)Îr.

2) Marrëdhënia nuk është antirefleksive, pasi kushti i kësaj vetie nuk është i plotësuar. Për shembull, (2, 2)Îr, por kjo nuk do të thotë se 2¹2.

3) Shqyrtoni të gjitha rastet e mundshme, duke treguar se relacioni r është simetrik:

	(a, b)Îr	(b, a)	(b, a)Îr?

4) Kjo lidhje nuk është antisimetrike, pasi (1, 2)Îr dhe (2,1)Îr, por nga kjo nuk del se 1=2.

5) Është e mundur të tregohet se relacioni r është kalimtar duke përdorur metodën e numërimit të drejtpërdrejtë.

	(a, b)Îr	(b, c)Îr	(a, c)	(a, c)Îr?

Si të përdorim paraqitjen e matricës

të përcaktojë vetitë e një relacioni binare

1. Refleksiviteti: Të gjitha janë në diagonalen kryesore; zerat ose njësitë tregohen me yll.

.

2. Anti-refleksiviteti: Të gjitha zerat në diagonalen kryesore.

3. Simetria: Nëse .

4. Antisimetria: të gjithë elementët jashtë diagonales kryesore janë zero; mund të ketë edhe zero në diagonalen kryesore.

.

Operacioni "*" kryhet sipas rregullit të mëposhtëm: , Ku , .

5. Transitiviteti: Nëse . Veprimi “◦” kryhet sipas rregullit të zakonshëm të shumëzimit dhe është e nevojshme të merren parasysh: .

3.3 Marrëdhënie ekuivalente. Marrëdhënie e pjesshme e rendit.

Marrëdhënia e ekuivalencës është një zyrtarizim i situatës kur flasim për ngjashmërinë (ngjashmërinë) e dy elementeve të një grupi.

Përkufizimi 3.6. Raporti r aktiv A ka relacioni i ekuivalencës, nëse ajo refleksive, simetrike dhe kalimtare. Marrëdhënia e ekuivalencës a r b shpesh shënohet: a~ b.

Shembull 3. 8 . Marrëdhënia e barazisë në bashkësinë e numrave të plotë është një lidhje ekuivalente.

Shembull 3. 9 . Marrëdhënia "e njëjta lartësi" është një lidhje ekuivalente për një grup njerëzish X.

Shembull 3. 1 0 . Le të jetë ¢ bashkësia e numrave të plotë. Le të emërtojmë dy numra x Dhe y nga ¢ të krahasueshme në modulm(mО¥) dhe shkruani , nëse mbetjet e këtyre numrave pasi i pjesëtoni me m, pra dallimi ( x-y) i ndarë nga m.

Lidhja “e krahasueshme në modul m numra të plotë" është një lidhje ekuivalente në bashkësinë e numrave të plotë ¢. Me të vërtetë:

kjo lidhje është refleksive, sepse për " x΢ kemi x-x=0, dhe për këtë arsye pjesëtohet me m;

kjo lidhje është simetrike, sepse nëse ( x-y) i ndarë nga m, pastaj ( y-x) është gjithashtu i pjesëtueshëm me m;

kjo lidhje është kalimtare, sepse nëse ( x-y) i ndarë nga m, pastaj për disa numra të plotë t 1 kemi https://pandia.ru/text/78/250/images/image025_23.gif" width="73" height="24 src=">, nga këtu , dmth ( x-z) i ndarë nga m.

Përkufizimi 3.7. Raporti r aktiv A ka lidhje e pjesshme e rendit, nëse ajo refleksive, antisimetrike dhe kalimtare dhe tregohet me simbolin °.

Rendi i pjesshëm është i rëndësishëm në situatat kur duam të karakterizojmë disi përparësinë. Me fjalë të tjera, vendosni në cilat kushte të konsideroni një element të grupit si superior ndaj një tjetri.

Shembull 3. 11 . Qëndrimi x£ y ekziston një lidhje e pjesshme e rendit në bashkësinë e numrave realë. ,

Shembull 3. 1 2 . Në bashkësinë e nëngrupeve të disa grupeve universale U qëndrim AÍ B ekziston një lidhje e pjesshme e rendit.

Shembull 3. 1 3 . Skema e organizimit të vartësisë në një institucion është një marrëdhënie e rendit të pjesshëm në një grup pozicionesh.

Prototipi i një relacioni të rendit të pjesshëm është koncepti intuitiv i një marrëdhënie preference (precedence). Një lidhje preference identifikon një klasë problemesh që mund të kombinohen si problemi i problemit të zgjedhjes objekti më i mirë .

Formulimi i problemit: le të ketë një koleksion objektesh A dhe kërkohet krahasimi i tyre sipas preferencës, d.m.th., vendosja e relacionit të preferencës në grup A dhe identifikoni objektet më të mira.

Marrëdhënie preferenciale P, e cila mund të përkufizohet si " aPb, a, bÎ AÛ objekt a jo më pak e preferueshme se objekti b"është refleksiv dhe antisimetrik në kuptim (çdo objekt nuk është më i keq se vetvetja, dhe nëse objekti a jo me keq b Dhe b jo me keq a, atëherë ato janë të njëjta në preferencë). Është e natyrshme të supozohet se marrëdhënia P në mënyrë kalimtare (edhe pse në rastin kur, për shembull, preferencat diskutohen nga një grup njerëzish me interesa të kundërta, kjo pronë mund të cenohet), d.m.th. P– lidhje e pjesshme e rendit.

Një nga mënyrat e mundshme për të zgjidhur problemin e krahasimit të objekteve sipas preferencës është duke filluar , d.m.th., renditja e objekteve në përputhje me preferencën ose ekuivalencën në rënie. Si rezultat i renditjes, ne identifikojmë objektet "më të mira" ose "më të këqija" nga pikëpamja e marrëdhënies së preferencës.

Zonat e përdorimit probleme rreth problemit të zgjedhjes së objektit më të mirë: teoria e vendimeve, matematika e aplikuar, teknologjia, ekonomia, sociologjia, psikologjia.