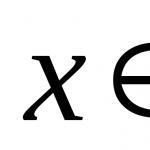Primjeri su binarna relacija i njezine karakteristike. Binarne relacije i njihova svojstva

Kartezijanski produkt dva seta x I Y naziva skup svatko uređeni parovi ( x, g ) takav da
, A
.

Primjer 1 . Neka .

zatim, .

Očito je da
, tj. Kartezijev umnožak operacije skupova nije komutativan.

Kartezijev produkt skupova
naziva skup
svi naručeni setovi
takav daAko
, tada se označava Kartezijev produkt
.

Reći ćemo da je dopisivanje dano q između setova x I Y, ako je zadana uređena trojka
, Gdje
.Gomila x naziva se područje polaska, i Y– područje prispijeća korespondencije q(označiti
). Svaki element g u paru sa
naziva se slika elementa x (x– prototip elementa g) za ovu korespondenciju q.

Dopisivanje
nazvao prikaz postavlja x u mnogim Y, ako je svaki element
ima sliku
, tj.

Prikaz
nazvao funkcionalni , ako je svaki element
Ima jedini slika
:. Mnogo slika za određeni prikaz
označen sa
:.

Ako skup
poklapa sa skupom Y, onda to kažu
prikazuje na gomila Y.

Dopisivanje
nazvao jedan na jedan (bijekcija) , ako je a) preslikavanje; b) funkcionalno; c) prikazi x"na" snimanju Y; d) iz stanja
trebao bi
.

Drugim riječima,
je bijekcija ako svaki element
ima jednu sliku
, i svaki element
ima jedan prototip
s ovim prikazom:

(1.2)

1.2.2 Definicija binarne relacije

Definicija. Kažu to na mnogima x data binarna relacija R, ako je dan podskup Kartezijevog produkta
(oni.
).

Primjer 2 . Neka
Postavimo ga na x sljedeće odnose:

– odnos jednakosti;

– odnos prvenstva;

podjeljeno sa – odnos djeljivosti.

Svi ovi odnosi specificirani su pomoću karakterističnog svojstva. Elementi ovog odnosa navedeni su u nastavku:

Činjenica da je par ( x, g) pripada ovoj relaciji R, pisat ćemo:
ili xRy. Na primjer, za odnos Q unos 4 Q 2 znači 4 je djeljiv sa 2, tj.

Domena definicije
binarna relacija R naziva skup
Raspon vrijednosti
naziva skup

Da, za vezu R iz primjera 2 domena definicije je skup
, a raspon vrijednosti je
.

1.2.3 Metode za specificiranje binarne relacije

Binarna relacija može se specificirati navođenjem karakterističnog svojstva ili navođenjem svih njegovih elemenata. Vizualniji načini specificiranja binarne relacije su relacijski graf, relacijski dijagram, relacijski graf, relacijska matrica.

Raspored odnosi su prikazani u kartezijevom koordinatnom sustavu; horizontalna os označava domenu definicije, vertikalna os označava skup relacijskih vrijednosti; element relacije ( x,y) odgovara točki na ravnini s tim koordinatama. Na sl. 1.7,a) prikazuje grafikon omjera Q primjer 2.

Shema odnosi se prikazuju pomoću dvije okomite crte, od kojih lijeva odgovara domeni definiranja odnosa, a desna skupu vrijednosti odnosa. Ako je element ( x,y) pripada relaciji R, zatim odgovarajuće točke iz
I
spojeni ravnim segmentom. Na sl. 1.7,b) prikazuje dijagram odnosa Q iz primjera 2.

Grafikon odnos
konstruiran je na sljedeći način. Točke – elementi skupa – prikazane su na ravnini bilo kojim redoslijedom x. Par bodova x I na spojen je lukom (crta sa strelicom) ako i samo ako je par ( x,y) pripada relaciji R. Na sl. 1.8,a) prikazuje relacijski graf Q primjer 2.

Neka
. Matrica odnos
Ima n linije i n stupaca, i njegov element određuje pravilo:

Slika 1.8b) prikazuje matricu odnosa Q primjer 2.

Povezane definicije

Svojstva odnosa

Binarne relacije mogu imati različita svojstva, kao npr

Vrste odnosa

Refleksivna tranzitivna relacija naziva se relacija kvazi-poretka.
Refleksivna simetrična tranzitivna relacija naziva se relacija ekvivalencije.
Refleksivna antisimetrična tranzitivna relacija naziva se relacija (djelomičnog) reda.
Antirefleksivna antisimetrična tranzitivna relacija naziva se relacija strogog reda.
Potpuna antisimetrična (za bilo koji x, y xRy ili yRx vrijedi) tranzitivna relacija naziva se linearna relacija reda.
Antirefleksni asimetrični odnos naziva se odnos dominacije.

Vrste dvostrukih odnosa

Obrnuti stav [navesti] (relacija inverzna R) je binarna relacija koja se sastoji od parova elemenata (y, x) dobivenih permutiranjem parova elemenata (x, y) dane relacije R. Označava se s: R −1. Za ovu relaciju i njen inverz vrijedi sljedeća jednakost: (R −1) −1 = R.
Recipročni odnosi(recipročni odnosi) - odnosi koji su međusobno inverzni. Raspon vrijednosti jednog od njih služi kao raspon definicije drugog, a raspon definicije prvog služi kao raspon vrijednosti drugog.
Reflektivni stav- binarna relacija R definirana na određenom skupu i karakterizirana time da je za bilo koji x iz tog skupa element x u odnosu R prema samom sebi, odnosno za bilo koji element x iz tog skupa vrijedi xRx. Primjeri refleksivnih odnosa: jednakost, istovremenost, sličnost.
Antirefleksni stav(Ireflektivna relacija, imajte na umu da kao što se antisimetrija ne podudara s asimetrijom, irefleksivnost se ne podudara s nerefleksivnošću.) - dvomjesna relacija R definirana na određenom skupu i karakterizirana time da za bilo koji element x ovog skupa nije točno da je u odnosu R prema sebi (nije točno da xRx), odnosno moguće je da element skupa nije u odnosu R prema sebi. Primjeri nerefleksivnih stavova: "brinuti se", "zabavljati", "nervozan".
Tranzitivni odnos- binarna relacija R, definirana na određenom skupu i karakterizirana time da za bilo koji x, y, z tog skupa, xRy i yRz impliciraju xRz (xRy&yRzxRz). Primjeri tranzitivnih odnosa: “više”, “manje”, “jednako”, “slično”, “iznad”, “sjever”.
Neprijelazni odnos [navesti] - binarna relacija R definirana na određenom skupu i karakterizirana time da za bilo koji x, y, z ovog skupa xRy i yRz ne impliciraju xRz ((xRy&yRzxRz)). Primjer neprelazne relacije: "x je otac od y"
Simetrični odnos- dvomjesna relacija R, definirana na određenom skupu i karakterizirana time da za bilo koje elemente x i y tog skupa, iz činjenice da je x prema y u odnosu R (xRy), slijedi da je y u istom odnos prema x ( yRx). Primjer simetričnih odnosa može biti jednakost (=), odnos jednakosti, sličnosti, istovremenosti, neki odnosi srodstva (npr. odnos bratstva).
Antisimetrična relacija- dvomjesna relacija R, definirana na određenom skupu i karakterizirana time da za bilo koje x i y iz xRy i xR −1 y slijedi x = y (to jest, R i R −1 su zadovoljeni istovremeno samo za članove koji su međusobno jednaki).
Asimetričan odnos [navesti] je dvomjesna relacija R, definirana na određenom skupu i karakterizirana time da za bilo koje x i y, xRy implicira yRx. Primjer: odnos "više od" (>) i "manje od" (<).
Relacija ekvivalencije(odnos identiteta [ navesti], odnos tipa jednakosti) je dvomjesni odnos R između objekata x i y u predmetnom području D, koji zadovoljava sljedeće aksiome (uvjete): Dakle, odnos tipa jednakosti je istovremeno refleksivan, simetričan i tranzitivan. Primjeri: jednakost, jednaka kardinalnost dva skupa, razmjenjivost dobara na tržištu, sličnost, istovremenost. Primjer relacije koja zadovoljava aksiom (3), ali ne zadovoljava aksiome (1) i (2): "više."
Odnosi reda- relacije koje imaju samo neka od tri svojstva relacije ekvivalencije. Konkretno, odnos koji je refleksivan i tranzitivan, ali asimetričan (na primjer, "nema više") tvori "labav" poredak. Odnos je tranzitivan, ali nerefleksivan i asimetričan (npr. "manje od") - "strogi" poredak.
Funkcija- dvostruki odnos R, definiran na određenom skupu, karakteriziran time da za svaku vrijednost x odnos xRy g. Primjer: " g otac x" Svojstvo funkcionalnosti relacije R je napisan kao aksiom: ( xRy I xRz)→(g≡z). Budući da svaka vrijednost x u izrazima xRy I xRz odgovara istoj vrijednosti, tada g I z poklopiti, pokazati se istim. Funkcionalna relacija je jedinstvena, jer svaka vrijednost x ima relaciju xRy odgovara samo jednoj jedinoj vrijednosti g, ali ne obrnuto.
Bijekcija(one-place relation) - dvomjesna relacija R, definiran na određenom skupu, karakteriziran time što u njemu svaka vrijednost x odgovara jednoj vrijednosti na, i svaka vrijednost na odgovara jednoj vrijednosti x. Relacija jedan na jedan poseban je slučaj relacije jedan na jedan.
Srodni odnos- ovo je dvomjesna relacija R, definiran na određenom skupu, karakteriziran time da za bilo koja dva različita elementa x I na ovog skupa, jedan od njih je u odnosu R drugome (to jest, jedan od dva odnosa je zadovoljen: xRy ili yRx). Primjer: relacija "manje od" (<).

Operacije na odnosima

Budući da su relacije definirane na fiksnom paru skupova , , podskupovi skupa , skup svih ovih relacija tvori Booleovu algebru s obzirom na operacije unije, presjeka i zbrajanja relacija. Konkretno, za proizvoljno

Često se, umjesto o odnosima spajanja, presijecanja i nadopunjavanja, govori o njihovoj disjunkciji, konjunkciji i negaciji.

Na primjer, , , tj. unija striktne relacije reda s relacijom jednakosti koincidira s nestrogom relacijom reda, a njihovo sjecište je prazno.

Osim navedenih, važne su i operacije inverzije i množenja relacija definirane na sljedeći način.

Ako je tada inverzna relacija relacija definirana na paru i sastoji se od onih parova za koje je . Na primjer, .

Neka sada,. Proizvod odnosa je odnos takav da

Ako je , i , tada je umnožak relacija nedefiniran. Ako promatramo relacije definirane na nekom skupu, tada se takva situacija ne pojavljuje.

Na primjer, razmotrite strogu relaciju reda definiranu na skupu prirodnih brojeva. Lako je to primijetiti

Binarne relacije nazivamo komutativnim ako . Lako je vidjeti da za bilo koju binarnu relaciju definiranu na , gdje simbol označava jednakost definiranu na . Međutim, jednakost nije uvijek pravedna.

Važe sljedeći identiteti:

Imajte na umu da analozi posljednja dva identiteta ne vrijede.

Neka svojstva relacije mogu se odrediti korištenjem relacijskih operacija:

vidi također

Književnost

A. I. Malcev. Algebarski sustavi. - M.: Znanost, 1970.

Zaklada Wikimedia. 2010.

- dvomjesni predikat na zadanom skupu. Pod B. o. ponekad shvaćen kao podskup skupa uređenih parova (a, 6) elemenata danog skupa A. B. o. poseban slučaj odnosa. Neka bude. Ako, tada se za element kaže da je u binarnom obliku... ... Matematička enciklopedija

U logici, nešto što, za razliku od svojstva, ne karakterizira pojedinačni predmet, već par, tri itd. stavke. Tradicionalna logika nije uzimala u obzir O.; u modernoj logici O. iskazna je funkcija dviju ili više varijabli. Binarni... Filozofska enciklopedija

stav- ODNOS je skup uređenih n ok jedinki (gdje je n 1), tj. dvojke, trojke itd. Broj n naziva se “lokalnost”, ili “arnost”, O. i, prema tome, govore o n lokalnih (n arno) O. Tako se, na primjer, dvostruko O. naziva... ... Enciklopedija epistemologije i filozofije znanosti

U teoriji potrošača, ovo je formalni opis potrošačeve sposobnosti da usporedi (poredi prema poželjnosti) različite skupove dobara (potrošačke pakete). Da bi se opisao odnos preferencija, nije potrebno mjeriti poželjnost... ... Wikipedia

Ovaj izraz ima i druga značenja, vidi stav. Relacija je matematička struktura koja formalno definira svojstva različitih objekata i njihove odnose. Odnosi se obično klasificiraju prema broju objekata koji se povezuju... Wikipedia

Ovaj izraz ima i druga značenja, vidi stav. Odnos u logici prvog reda prema dva ili više predikata argumenata (više predikata), dva ili više svojstava predikata. Znak odnosa: R.[navedite] U smislu odnosa... ... Wikipedia, A.I. Shirokov. Priručnik je sedmi dio dijela “Osnovne teorijske konstrukcije skupova” akademske discipline “Diskretna matematika”. Uvodi i analizira takve... e-knjiga

Neka R je neka binarna relacija na skupu X, a x, y, z su bilo koji njeni elementi. Ako je element x u odnosu R s elementom y, tada pišite xRy.

1. Odnos R na skupu X naziva se refleksivnim ako je svaki element skupa u tom odnosu sam sa sobom.

R - refleksivno na X<=>xRx za bilo koje x€ X

Ako je relacija R refleksivna, tada postoji petlja na svakom vrhu grafa. Na primjer, odnosi jednakosti i paralelnosti za segmente su refleksivni, ali odnosi okomitosti i "duže" nisu refleksivni. To se odražava na grafikonima na slici 42.

2. Relacija R na skupu X naziva se simetričnom ako iz činjenice da je element x u danom odnosu s elementom y, slijedi da je element y u istom odnosu s elementom x.

R - simetrično na (xYay =>y Rx)

Graf simetrične relacije sadrži uparene strelice koje idu u suprotnim smjerovima. Relacije paralelnosti, okomitosti i jednakosti za segmente su simetrične, ali relacija “duži” nije simetrična (slika 42).

3. Relacija R na skupu X naziva se antisimetričnom ako za različite elemente x i y iz skupa X, iz činjenice da je element x u zadanoj relaciji s elementom y, slijedi da element y nije u tom odnosu s elementom x.

R - antisimetrično na X « (xRy i xy ≠ yRx)

Napomena: crtica iznad označava negaciju izjave.

U antisimetričnom relacijskom grafu dvije točke mogu biti povezane samo jednom strelicom. Primjer takve relacije je relacija “dulje” za segmente (slika 42). Relacije paralelizma, okomitosti i jednakosti nisu antisimetrične. Postoje odnosi koji nisu ni simetrični ni antisimetrični, na primjer odnos “biti brat” (slika 40).

4. Relacija R na skupu X naziva se tranzitivnom ako iz činjenice da je element x u zadanoj relaciji s elementom y, a element y u toj relaciji s elementom z, slijedi da je element x u zadana relacija s elementom Z

R - tranzitivno na A≠ (xRy i yRz=> xRz)

U grafovima relacija “duže”, paralelnosti i jednakosti na slici 42 možete primijetiti da ako strelica ide od prvog elementa prema drugom i od drugog prema trećem, onda sigurno postoji strelica koja ide od prvog elementa. element trećem. Ovi odnosi su tranzitivni. Okomitost segmenata nema svojstvo tranzitivnosti.

Postoje i druga svojstva odnosa između elemenata istog skupa koja ne razmatramo.

Ista relacija može imati više svojstava. Tako je, na primjer, na skupu segmenata odnos “jednak” refleksivan, simetričan, tranzitivan; relacija “više” je antisimetrična i tranzitivna.

Ako je relacija na skupu X refleksivna, simetrična i tranzitivna, onda je to relacija ekvivalencije na tom skupu. Takve relacije dijele skup X na klase.

Ti se odnosi očituju, na primjer, prilikom izvršavanja zadataka: “Uzmi trake jednake duljine i rasporedi ih u skupine”, “Rasporedi kuglice tako da svaka kutija sadrži kuglice iste boje.” Relacije ekvivalencije („biti jednake duljine“, „biti iste boje“) određuju u ovom slučaju podjelu skupova pruga i loptica na klase.

Ako je relacija na skupu 1 tranzitivna i antisimetrična, tada se naziva relacija reda na tom skupu.

Skup sa zadanom relacijom reda naziva se uređen skup.

Na primjer, prilikom ispunjavanja zadataka: "Usporedite trake po širini i rasporedite ih od najuže prema najširoj", "Usporedite brojeve i rasporedite kartice s brojevima", djeca poredaju elemente skupova traka i kartica s brojevima. korištenje odnosa reda; “biti širi”, “pratiti”.

Općenito, odnosi ekvivalencije i reda igraju veliku ulogu u formiranju kod djece ispravnih ideja o klasifikaciji i poretku skupova. Osim toga, postoje mnogi drugi odnosi koji nisu niti odnosi ekvivalencije niti odnosi reda.

6. Što je karakteristično svojstvo skupa?

7. U kakvim odnosima mogu postojati skupovi? Dajte objašnjenja za svaki slučaj i oslikajte ih Eulerovim kružnicama.

8. Definirajte podskup. Navedite primjer skupova od kojih je jedan podskup drugoga. Napiši njihov odnos pomoću simbola.

9. Definirajte jednake skupove. Navedite primjere dva jednaka skupa. Napiši njihov odnos pomoću simbola.

10. Definirajte sjecište dva skupa i oslikajte ga Eulerovim kružnicama za svaki pojedini slučaj.

11. Definirajte uniju dvaju skupova i oslikajte je pomoću Eulerovih kružnica za svaki pojedini slučaj.

12. Definirajte razliku između dva skupa i oslikajte je pomoću Eulerovih kružnica za svaki pojedini slučaj.

13. Definirajte komplement i prikažite ga Eulerovim kružnicama.

14. Što se naziva podjela skupa na klase? Navedite uvjete za ispravno razvrstavanje.

15. Što se naziva korespondencija između dva skupa? Navedite metode za specificiranje korespondencija.

16. Koju vrstu korespondencije nazivamo jedan-na-jedan?

17. Koji se skupovi nazivaju jednakima?

18. Koji se skupovi nazivaju ekvivalentnim?

19. Navedite načine definiranja relacija na skupu.

20. Koja se relacija na skupu naziva refleksivnom?

21. Koja se relacija na skupu naziva simetričnom?

22. Koja se relacija na skupu naziva antisimetričnom?

23. Koja se relacija na skupu naziva tranzitivnom?

24. Definirajte relaciju ekvivalencije.

25. Definirajte relaciju reda.

26. Koji se skup naziva uređenim?

Jezik T-SQL u SQL Serveru temelji se na standardnom jeziku SQL, koji se temelji na relacijskom modelu, koji se opet temelji na matematičkim osnovama kao što su teorija skupova i logika predikata. Ovaj članak ispituje temeljnu temu iz teorije skupova: svojstva odnosa na skupovima. Čitatelji mogu koristiti predložene T-SQL kodove za provjeru prisutnosti određenih svojstava određenih odnosa. Međutim, također možete pokušati napisati vlastite verzije skripti (kako biste utvrdili ima li relacija određeno svojstvo) prije primjene rješenja opisanih u ovom članku.

Skupovi i relacije

Georg Cantor, tvorac teorije skupova, definira skup kao "ujedinjenje u određenu cjelinu M zbirke određenih jasno prepoznatljivih objekata m naše kontemplacije ili mišljenja (koji će se zvati elementi skupa M)." Elementi skupa mogu biti predmeti proizvoljne prirode: ljudi, brojevi, pa čak i sami skupovi. Simboli ∈ i ∉ označavaju redom operatore koji odražavaju pripadnost (pojavljivanje, članstvo) i ne-pripadnost elementa u skupu. Dakle, oznaka x ∈ V znači da je x element skupa V, a oznaka x ∉ V znači da x nije element skupa V.

Binarna relacija na skupu je skup uređenih parova elemenata izvornog skupa. Dakle, za skup elemenata V = (a, b, c), binarna relacija R na danom skupu V bit će proizvoljan podskup skupa svih uređenih parova Kartezijevog produkta V × V = ((a, a), (a, b), (a , c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c) ). Relacija R = ((a, b), (b, c), (a, c)) je važeća binarna relacija na V. Možemo reći da je a povezan s b pomoću R. Pretpostavimo da je R = ((a , b ), (b, c), (c, d)). Takav R nije prihvatljiva relacija na V, budući da par (c, d) ne pripada Kartezijevom umnošku V × V. Imajte na umu da redoslijed kojim su navedeni elementi uključeni u skup nije važan. Skup V može biti specificiran kao (a, b, c) ili kao (b, a, c) i tako dalje. Međutim, važan je poredak u uređenim parovima, kao što je (a, b) binarne relacije; dakle (a, b) ≠ (b, a).

Kao realističniji primjer binarne relacije, razmotrite skup F članova obitelji: (Itsik, Mickey, Inna, Mila, Gabi). Mickey je Itzikov brat blizanac, Inna mu je starija sestra, Mila mu je majka, a Gabi otac. Primjer relacije R na skupu F bio bi: "je brat." Elementi ovog odnosa su ((Itsik, Mickey), (Mickey, Itzik), (Itsik, Inna), (Mickey, Inna)). Napominjemo da se uređeni par (Itsik, Inna) pojavljuje u R, ali par (Inna, Itsik) ne. Iako je Itzik Innin brat, ona nije njegov brat.

Svojstva relacija na skupovima

Sad kad smo osvježili razumijevanje skupova i relacija, prijeđimo na temu članka – svojstva relacija na skupovima. Na primjer podaci, upotrijebite kod u Ispisu 1 za izradu tablica V i R. V će predstavljati skup, a R će predstavljati binarnu relaciju na njemu. Upotrijebite kod u Ispisu 2 za stvaranje procedure ClearTables koja će obrisati obje ove tablice od zapisa prije nego što ih popuni novim oglednim podacima. Na kraju, upotrijebite kod u Ispisima 3, 4 i 5 za popunjavanje tablica V i R s različitim skupovima podataka za testiranje (nazvat ćemo ih ogledni podaci 1, 2 i 3).

Refleksivnost. Relacija R na skupu V je refleksivna ako za bilo koji element v skupa V, v ∈ V, slijedi da (v, v) ∈ R, odnosno par (v, v) uvijek pripada R. I relacija R na V nije refleksivna, ako postoji element v ∈ V takav da je par (v, v) ∉ R. Razmotrimo ponovno primjer skupa F - članovi moje obitelji.

Odnos "biti istih godina" na F očito je refleksivan. Elementi veze bit će sljedeći parovi: ((Itsik, Itsik), (Itsik, Mickey), (Mickey, Mickey), (Mickey, Itzik), (Inna, Inna), (Mila, Mila), (Gabi) , Gabi)).

Počnimo pisati T-SQL upit prema tablicama V i R (koje predstavljaju skup i relaciju na ovom skupu), provjeravajući je li R refleksivan:

IZABERI
SLUČAJ
KADA POSTOJI
(SELECT v, v IZ dbo.V
OSIM
SELECT r1, r2 FROM dbo.R)
Onda ne"
INAČE "Da"
KRAJ KAO refleksivan

Prvi podupit u operaciji EXCEPT vraća skup svih uređenih parova (v, v) za sve retke tablice V. Drugi podupit vraća skup uređenih parova (r1, r2) - sve redove tablice R. Operacija EXCEPT će stoga vratiti sve uređene parove koji se pojavljuju u prvom i nedostaju u drugom skupu. Predikat EXISTS potreban je za provjeru postojanja barem jednog zapisa u skupu rezultata. Ako postoji barem jedan takav zapis, onda će izraz CASE vratiti "Ne" (nema refleksivnosti), ali i "Da" u suprotnom (postoji refleksivnost).

Pogledajte tri primjera skupa podataka u Ispisima 3, 4 i 5 i pokušajte odrediti koji bi imali reflektirajući odnos bez pokretanja upita. Odgovori su dati dalje u tekstu članka.

Nereflektirajuće. Relacija R na skupu V naziva se irefleksivnom (ne treba je brkati s nerefleksivnošću) ako za svaki element v ∈ V slijedi (v, v) ∉ R. Relacija nije irefleksivna ako postoji element v ∈ V za koje je (v, v) ∈ R. Primjer irefleksivne relacije na skupu F članova moje obitelji je relacija "biti roditelj", budući da nitko ne može biti sam sebi roditelj. Članovi ove relacije na F bit će sljedeći parovi: ((Mila, Itzik), (Mila, Mickey), (Mila, Inna), (Gabi, Itzik), (Gabi, Mickey), (Gabi, Inna)) .

Sljedeći upit provjerava je li relacija R na V nerefleksivna:

IZABERI
SLUČAJ
KADA POSTOJI
(SELECT * FROM dbo.R
GDJE je r1 = r2)
Onda ne"
INAČE "Da"
KRAJ KAO nerefleksivan

Strani ključevi u definiciji tablice R uvedeni su kako bi se osiguralo da samo elementi iz V mogu sačinjavati atribute r1 i r2 zapisa R. Dakle, sve što preostaje je provjeriti postoje li zapisi u R s odgovarajućim atributima r1 i r2. Ako se takav unos pronađe, relacija R nije irefleksivna; ako nema unosa, ona je irefleksivna.

Simetrija. Relacija R na skupu V naziva se simetričnom ako je, zajedno s (r1, r2) ∈ R, uvijek zadovoljeno (r2, r1) ∈ R. Relacija nije simetrična ako postoji neki par (r1, r2) ∈ R za koje je (r2, r1) ∉ R. Na skupu F članova obitelji Ben-Gan, relacija "je brat od" bila bi primjer simetrične relacije. Parovi ove relacije bit će sljedeći skupovi: ((Itsik, Mickey), (Itsik, Inna), (Mickey, Itzik), (Mickey, Inna), (Inna, Itzik), (Inna, Mickey)).

Sljedeći upit provjerava je li relacija R prema V simetrična:

IZABERI
SLUČAJ
KADA POSTOJI
(SELECT r1, r2 IZ dbo.R
OSIM
SELECT r2, r1 IZ dbo.R)
Onda ne"
INAČE "Da"
KRAJ KAO simetričan

Kod zahtjeva koristi operaciju EXCEPT. Prvi podupit operacije EXCEPT vraća skup uređenih parova (r1, r2) - zapisa tablice R, a drugi - skup uređenih parova (r2, r1) za svaki zapis R. Ako je relacija R na skup V nije simetričan, tada će operacija EXCEPT vratiti neprazan skup rezultata, a predikat EXISTS, odnosno vrijednost TRUE i, konačno, izraz CASE će vratiti "Ne".

Ako je odnos simetričan, tada će CASE izraz dati "Da".

Asimetrija. Relacija R na skupu V je asimetrična (ovo svojstvo ne treba brkati s asimetrijom) ako za svaki skup (r1, r2) ∈ R, u kojem je r1 ≠ r2, vrijedi (r2, r1) ∉ R. primjer asimetrične relacije na skupu F članova autorove obitelji imat će odnos "biti roditelj" koji je gore opisan. Kao vježbu, pokušajte smisliti primjer relacije na nepraznom skupu koji je i simetričan i asimetričan. Rješenje potražite u primjerima podataka u ovom članku.

IZABERI
SLUČAJ
KADA POSTOJI
(SELECT r1, r2 FROM dbo.R WHERE r1 r2
PRESJECATI
SELECT r2, r1 FROM dbo.R WHERE r1 r2)
Onda ne"
INAČE "Da"
KRAJ KAO asimetričan

Kod koristi operaciju INTERSECT. Prvi podupit u ovoj operaciji vraća uređeni par (r1, r2) za svaki zapis tablice R u kojem je r1 r2.

Drugi podupit operacije INTERSECT vraća uređeni par (r2, r1) za svaki zapis tablice R u kojem je r1 r2. Ako skup rezultata (rezultat presjeka ovih skupova) uključuje barem jedan zapis, to će značiti da R nije asimetričan; inače je R asimetričan.

Tranzitivnost. Relacija R na skupu V je tranzitivna ako uključivanje (a, b) ∈ R i (b, c) ∈ R uvijek implicira da (a, c) ∈ R. Primjer tranzitivne relacije na skupu članova obitelji F bi bila relacija "je li brat ili sestra" o čemu je gore bilo riječi.

Kod u nastavku testira tranzitivnost relacije R:

IZABERI
SLUČAJ
KADA POSTOJI
(IZABERI *
OD dbo.R KAO RA
UNUTARNJI SPOJ dbo.R AS RB
NA RA.r2 = RB.r1
LIJEVI VANJSKI SPOJ dbo.R KAO RC
NA RA.r1 = RC.r1 I RB.r2 = RC.r2
GDJE JE RC.r1 NULL)
Onda ne"
INAČE "Da"
KRAJ KAO prijelazan

Kod prvo koristi unutarnje spajanje između dvije instance R-a za odabir samo onih redaka gdje r2 u prvoj instanci odgovara r1 u drugoj instanci. Drugo, kod koristi lijevo vanjsko spajanje s trećom instancom tablice R, prema kojoj je r1 prve instance od R isti kao r1 treće instance, a r2 druge instance isti je kao r2 od treći. Ako postoji barem jedan red rezultata u unutarnjem podupitu (uvjet odabira za treću instancu: r1 je Null), to znači da relacija nije tranzitivna; inače je relacija R tranzitivna.

Relacija ekvivalencije. Relacija ekvivalencije je relacija koja istovremeno ima svojstva refleksivnosti, simetrije i tranzitivnosti. Možete upotrijebiti gore predložene upite da zasebno provjerite prisutnost svakog svojstva: ako relacija ima sva tri, tada bismo trebali zaključiti da vrijedi relacija ekvivalencije. Dodatno, možete upotrijebiti kod u Ispisu 6 za testiranje svih svojstava relacije R na skupu V o kojima se raspravljalo ranije u članku, uključujući testiranje svojstva relacije ekvivalencije. Ako pokrenete Ispis 6 na oglednim podacima 1, 2 i 3 (izvedenim iz Ispisa 3, 4, odnosno 5), dobit ćete rezultate prikazane u tablicama 1, 2 i 3.

Povratak na osnove T-SQL

Dakle, ispitali smo temeljnu temu iz matematičke teorije skupova: svojstva odnosa na skupovima. Predložio sam T-SQL test kodove za testiranje svojstava neke relacije predstavljene tablicom R (uređeni parovi elemenata) na skupu elemenata predstavljenih tablicom V.

Korištenje osnovnih T-SQL konstrukata pomoglo nam je da pravilno konfiguriramo i primijenimo alate ovog jezika za bolje razumijevanje svojstava relacija na skupovima.

Itzik Ben-Gan ( [e-mail zaštićen]) - nastavnik i savjetnik, autor knjiga o T-SQL-u, ima titulu SQL Server MVP

Predavanje 3.

klauzula 3. Relacije na skupovima. Svojstva binarnih odnosa.

3.1. Binarni odnosi.

Kada govore o odnosu dvoje ljudi, na primjer, Sergeja i Ane, misle da postoji određena obitelj kojoj pripadaju. Uređeni par (Sergej, Anna) razlikuje se od ostalih uređenih parova ljudi po tome što postoji neka vrsta odnosa između Sergeja i Ane (rođak, otac, itd.).

U matematici, između svih uređenih parova izravnog umnoška dva skupa A I B (A´ B) “posebni” parovi također se razlikuju zbog činjenice da između njihovih komponenti postoje neki “srodnički” odnosi koje drugi nemaju. Kao primjer, razmotrite set S studenti nekog sveučilišta i mnogi K tečajevi koji se tamo predaju. U izravnom proizvodu S´ K može se odabrati veliki podskup uređenih parova ( s, k) koji ima svojstvo: učenik s pohađa tečaj k. Konstruirani podskup odražava odnos "...sluša..." koji prirodno nastaje između skupova studenata i kolegija.

Za strogi matematički opis bilo koje veze između elemenata dva skupa, uvodimo koncept binarne relacije.

Definicija 3.1. Binarni (ili dvostruko )stav r između setova A I B poziva se proizvoljni podskup A´ B, tj.

Konkretno, ako A=B(tj. rÍ A 2), onda kažu da je r relacija na skupu A.

Elementi a I b se zovu komponente (ili koordinate ) odnos r.

Komentar. Dogovorimo se da se za označavanje odnosa između elemenata skupova koristi grčki alfabet: r, t, j, s, w itd.

Definicija 3.2. Domena definicije D r=( a| $ b, Što a r b) (lijeva strana). Raspon vrijednosti binarne relacije r naziva se skup R r=( b| $ a, Što a r b) (desni dio).

Primjer 3. 1. Neka su dana dva skupa A=(1; 3; 5; 7) i B=(2; 4; 6). Postavimo relaciju na sljedeći način t=(( x; g)Î A´ B | x+g=9). Ova relacija će se sastojati od sljedećih parova (3; 6), (5; 4) i (7; 2), koji se mogu napisati kao t=((3; 6), (5; 4), (7;2). ) ). U ovom primjeru D t=(3; 5; 7) i R t= B={2; 4; 6}.

Primjer 3. 2. Relacija jednakosti na skupu realnih brojeva je skup r=(( x; g) | x I g– realni brojevi i x jednaki g). Za ovaj odnos postoji posebna oznaka: “=”. Domena definicije poklapa se s domenom vrijednosti i skup je realnih brojeva, D r= R r.

Primjer 3. 3. Neka A– puno robe u trgovini, i B– skup realnih brojeva. Tada je j=(( x; g)Î A´ B | g– cijena x) – relacija skupova A I B.

Obratite li pozornost na primjer 3.1., primijetit ćete da je ova relacija prvo navedena u obliku t=(( x; g)Î A´ B | x+g=9), a zatim zapisano kao t=((3; 6), (5;4), (7;2)). Ovo sugerira da se relacije na skupovima (ili jednom skupu) mogu specificirati na različite načine. Pogledajmo načine definiranja binarnih odnosa.

Metode definiranja odnosa:

1) korištenje prikladnog predikata;

2) skup uređenih parova;

3) u grafičkom obliku: neka A I B– dva konačna skupa i r – binarna relacija između njih. Elementi ovih skupova prikazani su točkama na ravnini. Za svaki uređeni par relacija, r crta strelicu koja povezuje točke koje predstavljaju komponente para. Takav se objekt naziva usmjereni graf ili digraf, obično se nazivaju točke koje predstavljaju elemente skupova vrhovi grafa.

4) u obliku matrice: neka A={a 1, a 2, …, an) I B={b 1, b 2, …, bm), r – omjer na A´ B. Matrična reprezentacija r se naziva matrica M=[mij] veličina n´ m, definiran relacijama

Inače, matrični prikaz je prikaz relacije u računalu.

Primjer 3. 4. Neka su dana dva skupa A=(1; 3; 5; 7) i B=(2; 4; 6). Relacija je dana na sljedeći način t=(( x; g) | x+g=9). Definirajte ovu relaciju kao skup uređenih parova, digraf, u obliku matrice.

Riješenje. 1) t=((3; 6), (5; 4), (7; 2)) - je definicija relacije kao skupa uređenih parova;

2) odgovarajući usmjereni graf prikazan je na slici.

https://pandia.ru/text/78/250/images/image004_92.gif" width="125" height="117">. ,

Primjer 3. 5 . Kao primjer možemo razmotriti predloženi J. von Neumanna(1903. – 1957.) blok dijagram sekvencijalnog računala koje se sastoji od mnogo uređaja M:

Gdje a- ulazni uređaj, b– aritmetički uređaj (procesor), c- upravljački uređaj, d- Memorijski uređaj, e- izlazni uređaj.

Razmotrimo razmjenu informacija između uređaja mi I mj, koji su u odnosu r ako od uređaja mi informacija ulazi u uređaj mj.

Ova se binarna relacija može definirati ispisivanjem svih njezinih 14 uređenih parova elemenata:

Odgovarajući digraf koji definira ovu binarnu relaciju prikazan je na slici:

Matrična reprezentacija ove binarne relacije je:

. ,

Za binarne relacije teorijske operacije skupova definirane su na uobičajen način: unija, presjek, itd.

Uvedimo generalizirani koncept odnosa.

Definicija 3.3. n-mjesto (n-ari ) relacija r je podskup izravnog umnoška n skupovi, odnosno skup uređenih skupova ( tuples )

rÍ A 1 An={(a 1, …, an)| a 1O A 1Ù…Ù anÎ An}

Pogodno je definirati višemjesne relacije korištenjem relacijske tablice . Ovaj zadatak odgovara nabrajanju skupa n-to odnos r. Relacijske tablice naširoko se koriste u računalnoj praksi u relacijskim bazama podataka. Imajte na umu da se relacijske tablice koriste u svakodnevnoj praksi. Sve vrste proizvodnih, financijskih, znanstvenih i drugih izvješća često imaju oblik relacijskih tablica.

Riječ " relacijski“ dolazi od latinske riječi odnos, što prevedeno na ruski znači "stav". Stoga se u literaturi slovo koristi za označavanje odnosa R(latinski) ili r (grčki).

Definicija 3.4. Neka rÍ A´ B postoji stav prema A´ B. Tada se naziva omjer r-1 obrnuti odnos na zadani omjer r by A´ B, koji je definiran na sljedeći način:

r-1=(( b, a) | (a, b)Îr).

Definicija 3.5. Neka je r N A´ B postoji stav prema A´ B, a s N B´ C – odnos prema B´ C. Sastav odnosa s i r naziva se relacija t N A´ C, koji je definiran na sljedeći način:

t=s◦r= (( a, c)| $bÎ B, što (a, b)Îr I (b, c)Je).

Primjer 3. 6 . Neka i C=(, !, d, a). I neka je omjer r A´ B i omjer s na B´ C dati su u obliku:

r=((1, x), (1, g), (3, x)};

s=(( x,), (x, !), (g, d), ( g, à)}.

Nađite r-1 i s◦r, r◦s.

Riješenje. 1) Po definiciji r-1=(( x, 1), (g, 1), (x, 3)};

2) Koristeći se definicijom sastava dviju relacija dobivamo

s◦r=((1,), (1, !), (1, d), (1, a), (3,), (3, !)),

jer od (1, x)Îr i ( x,)Îs slijedi (1,)Îs◦r;

od (1, x)Îr i ( x, !)Îs slijedi (1, !)Îs◦r;

od (1, g)Îr i ( g, d)Îs slijedi (1, d)Îs◦r;

od (3, x)Îr i ( x, !)Îs slijedi (3, !)Îs◦r.

Teorem 3.1. Za sve binarne relacije vrijede sljedeća svojstva:

2) ;

3) - asocijativnost kompozicije.

Dokaz. Svojstvo 1 je očito.

Dokažimo svojstvo 2. Da bismo dokazali drugo svojstvo, pokazat ćemo da se skupovi zapisani na lijevoj i desnoj strani jednakosti sastoje od istih elemenata. Neka ( a; b) O (s◦r)-1 Û ( b; a) O s◦r Û $ c tako da ( b; c) O r i ( c; a) O s Û $ c tako da ( c; b) O r-1 i ( a; c) O s-1 Š ( a; b) O r -1◦s -1.

Dokažite svojstvo 3 sami.

3.2. Svojstva binarnih odnosa.

Razmotrimo posebna svojstva binarnih relacija na skupu A.

Svojstva binarnih odnosa.

1. Omjer r na A´ A nazvao reflektirajući , Ako ( a,a) pripada r za sve a iz A.

2. Relacija r naziva se antirefleksni , ako od ( a,b)Îr slijedi a¹ b.

3. Omjer r simetrično , ako je za a I b pripada A, od ( a,b)Ili slijedi da ( b,a)Îr.

4. Relacija r se naziva antisimetričan , ako je za a I b iz A, od pripadnosti ( a,b) i ( b,a) relacija r implicira da a=b.

5. Omjer r tranzitivno , ako je za a, b I c iz A iz činjenice da ( a,b)Îr i ( b,c)Îr, slijedi da ( a,c)Îr.

Primjer 3. 7. Neka A=(1; 2; 3; 4; 5; 6). Na ovom skupu je dana relacija rÍ A 2, koji ima oblik: r=((1, 1), (2, 2), (3, 3), (4; 4), (5; 5), (6; 6), (1; 2) ), (1; 4), (2; 1), (2; 4), (3; 5), (5; 3), (4; 1), (4; 2)). Koja svojstva ima ovaj odnos?

Riješenje. 1) Ovaj odnos je refleksivan, jer za svaki aÎ A, (a; a)Îr.

2) Odnos nije antirefleksivan, budući da uvjet ovog svojstva nije zadovoljen. Na primjer, (2, 2)Îr, ali to ne znači da je 2¹2.

3) Razmotrimo sve moguće slučajeve, pokazujući da je relacija r simetrična:

(a, b)Îr	(b, a)	(b, a)Îr?

4) Ova relacija nije antisimetrična, jer (1, 2)Îr i (2,1)Îr, ali iz toga ne slijedi da je 1=2.

5) Metodom izravnog nabrajanja moguće je pokazati da je relacija r tranzitivna.

(a, b)Îr	(b, c)Îr	(a, c)	(a, c)Îr?

Kako koristiti matričnu reprezentaciju

odrediti svojstva binarne relacije

1. Refleksivnost: Sve jedinice su na glavnoj dijagonali; nule ili jedinice označene su zvjezdicama.

2. Antirefleksivnost: Sve nule na glavnoj dijagonali.

3. Simetrija: ako .

4. Antisimetrija: svi elementi izvan glavne dijagonale su nula; na glavnoj dijagonali mogu biti i nule.

Operacija “*” izvodi se prema sljedećem pravilu: , Gdje , .

5. Tranzitivnost: ako . Operacija “◦” izvodi se prema uobičajenom pravilu množenja, a potrebno je voditi računa o: .

3.3 Relacija ekvivalencije. Odnos djelomičnog reda.

Relacija ekvivalencije je formalizacija situacije kada govorimo o sličnosti (istosti) dva elementa skupa.

Definicija 3.6. Omjer r na A Tamo je odnos ekvivalencije, ako refleksivna, simetrična i tranzitivna. Relacija ekvivalencije a r bčesto se označava: a~ b.

Primjer 3. 8 . Relacija jednakosti na skupu cijelih brojeva je relacija ekvivalencije.

Primjer 3. 9 . Relacija "iste visine" je relacija ekvivalencije na skupu ljudi x.

Primjer 3. 1 0 . Neka je ¢ skup cijelih brojeva. Imenujmo dva broja x I g od ¢ usporedivi po modulum(m O¥) i napišite , ako su ostaci tih brojeva nakon dijeljenja s m, tj. razlika ( x-g) podjeljeno sa m.

Relacija “usporediva po modulu m cijeli brojevi" je relacija ekvivalencije na skupu cijelih brojeva ¢. Doista:

ovaj odnos je refleksivan, jer za " xÎ¢ imamo x-x=0, pa je stoga djeljiv sa m;

ova relacija je simetrična, jer ako ( x-g) podjeljeno sa m, zatim ( g-x) također je djeljiv sa m;

ova relacija je tranzitivna, jer ako ( x-g) podjeljeno sa m, zatim za neki cijeli broj t 1 imamo https://pandia.ru/text/78/250/images/image025_23.gif" width="73" height="24 src=">, odavde , tj. ( x-z) podjeljeno sa m.

Definicija 3.7. Omjer r na A Tamo je relacija djelomičnog reda, ako refleksivna, antisimetrična i tranzitivna a označava se simbolom °.

Djelomični poredak je važan u situacijama kada želimo nekako okarakterizirati prvenstvo. Drugim riječima, odlučite pod kojim uvjetima smatramo da je jedan element skupa superiorniji od drugog.

Primjer 3. 11 . Stav x£ g na skupu realnih brojeva postoji relacija djelomičnog reda. ,

Primjer 3. 1 2 . U skupu podskupova nekog univerzalnog skupa U stav AÍ B postoji parcijalni odnos reda.

Primjer 3. 1 3 . Shema organizacije subordinacije u ustanovi je odnos djelomičnog reda u skupu položaja.

Prototip relacije djelomičnog reda je intuitivni koncept relacije preferencija (prethodstva). Odnos preferencija identificira klasu problema koji se mogu kombinirati kao problem izbora problem najbolji objekt .

Formulacija problema: neka bude zbirka predmeta A te ih je potrebno usporediti prema preferencijama, tj. postaviti relaciju preferencija na skupu A i identificirati najbolje objekte.

Odnos preferencija P, koji se može definirati kao " aPb, a, bÎ AÛ prigovaram a ne manje poželjan od objekta b"je refleksivan i antisimetričan u značenju (svaki objekt nije ništa gori od sebe, a ako objekt a ništa gore b I b ništa gore a, onda su iste u sklonosti). Prirodno je pretpostaviti da odnos P tranzitivno (iako u slučaju kada npr. o preferencijama raspravlja grupa ljudi sa suprotnim interesima, to svojstvo može biti narušeno), tj. P– parcijalni odnos reda.

Jedan od mogućih načina rješavanja problema usporedbe objekata po preferencijama je rangiranje , tj. poredanje objekata u skladu s opadajućom preferencijom ili ekvivalencijom. Kao rezultat rangiranja, identificiramo "najbolje" ili "najgore" objekte sa stajališta odnosa preferencija.

Područja upotrebe problemi oko problema izbora najboljeg objekta: teorija odlučivanja, primijenjena matematika, tehnologija, ekonomija, sociologija, psihologija.