Θεώρημα εργατικού δυναμικού για την κινητική ενέργεια. Referat

Κλιμωτή τιμή T, ίσο με το άθροισμακινητικές ενέργειες όλων των σημείων του συστήματος ονομάζεται κινητική ενέργεια του συστήματος.

Η κινητική ενέργεια είναι χαρακτηριστικό της μεταφορικής και περιστροφικής κίνησης του συστήματος. Η αλλαγή του επηρεάζεται από τη δράση εξωτερικών δυνάμεων, και δεδομένου ότι είναι βαθμωτή, δεν εξαρτάται από την κατεύθυνση κίνησης των τμημάτων του συστήματος.

Ας βρούμε την κινητική ενέργεια για διαφορετικές περιπτώσεις κίνησης:

1.Μεταφραστική κίνηση

Οι ταχύτητες όλων των σημείων του συστήματος είναι ίσες με την ταχύτητα του κέντρου μάζας. Τότε

Η κινητική ενέργεια του συστήματος κατά τη μεταφορική κίνηση είναι ίση με το μισό του γινόμενου της μάζας του συστήματος επί το τετράγωνο της ταχύτητας του κέντρου μάζας.

2. Περιστροφική κίνηση(εικ. 77)

Η ταχύτητα οποιουδήποτε σημείου στο σώμα:. Τότε

ή χρησιμοποιώντας τον τύπο (15.3.1):

Η κινητική ενέργεια ενός σώματος κατά την περιστροφή είναι ίση με το μισό γινόμενο της ροπής αδράνειας του σώματος σε σχέση με τον άξονα περιστροφής κατά το τετράγωνο της γωνιακής του ταχύτητας.

3. Επίπεδο-παράλληλη κίνηση

Με μια δεδομένη κίνηση, η κινητική ενέργεια είναι το άθροισμα της ενέργειας των μεταφορικών και περιστροφικών κινήσεων

Η γενική περίπτωση της κίνησης δίνει τον τύπο για τον υπολογισμό κινητική ενέργειαπαρόμοια με την τελευταία.

Κάναμε τον ορισμό του έργου και της ισχύος στην παράγραφο 3 του Κεφαλαίου 14. Εδώ θα εξετάσουμε παραδείγματα υπολογισμού του έργου και της ισχύος των δυνάμεων που δρουν σε ένα μηχανικό σύστημα.

1.Το έργο της βαρύτητας... Έστω, οι συντεταγμένες της αρχικής και τελικής θέσης του σημείου k του σώματος. Το έργο της δύναμης της βαρύτητας που ενεργεί σε αυτό το σωματίδιο βάρους θα είναι ... Τότε η πλήρης εργασία είναι:

όπου P είναι το βάρος του συστήματος των υλικών σημείων, είναι η κατακόρυφη μετατόπιση του κέντρου βάρους C.

2. Το έργο των δυνάμεων που ασκούνται σε ένα περιστρεφόμενο σώμα.

Σύμφωνα με τη σχέση (14.3.1), μπορεί να γραφτεί, αλλά το ds σύμφωνα με το Σχ. 74, λόγω της άπειρης μικρότητάς του, μπορεί να αναπαρασταθεί με τη μορφή - απείρως μικρή γωνία περιστροφής του σώματος. Τότε

Το μέγεθος που ονομάζεται ροπή.

Ο τύπος (19.1.6) μπορεί να ξαναγραφτεί ως

Το στοιχειώδες έργο είναι ίσο με το γινόμενο της ροπής και της στοιχειώδους περιστροφής.

Όταν γυρίζουμε σε μια τελική γωνία, έχουμε:

Αν η ροπή είναι σταθερή, τότε

και η ισχύς προσδιορίζεται από τη σχέση (14.3.5)

ως το γινόμενο της ροπής και της γωνιακής ταχύτητας του σώματος.

Το θεώρημα για τη μεταβολή της κινητικής ενέργειας που αποδείχθηκε για ένα σημείο (§ 14.4) θα ισχύει για οποιοδήποτε σημείο του συστήματος

Συνθέτοντας τέτοιες εξισώσεις για όλα τα σημεία του συστήματος και προσθέτοντάς τα ανά όρο, λαμβάνουμε:

ή, σύμφωνα με (19.1.1):

που είναι η έκφραση του θεωρήματος για την κινητική ενέργεια του συστήματος σε διαφορική μορφή.

Με την ενσωμάτωση (19.2.2) παίρνουμε:

Το θεώρημα για την αλλαγή της κινητικής ενέργειας στην τελική μορφή: η μεταβολή της κινητικής ενέργειας του συστήματος με κάποια από την τελική του μετατόπιση είναι ίση με το άθροισμα του έργου σε αυτή τη μετατόπιση όλων των εξωτερικών και εσωτερικών δυνάμεων που εφαρμόζονται στο σύστημα .

Να τονίσουμε ότι δεν αποκλείονται οι εσωτερικές δυνάμεις. Για ένα αμετάβλητο σύστημα, το άθροισμα του έργου όλων των εσωτερικών δυνάμεων είναι μηδέν και

Εάν οι περιορισμοί που επιβάλλονται στο σύστημα δεν αλλάξουν με την πάροδο του χρόνου, τότε οι δυνάμεις, εξωτερικές και εσωτερικές, μπορούν να χωριστούν σε ενεργές και σε αντιδράσεις περιορισμών και η εξίσωση (19.2.2) μπορεί τώρα να γραφεί:

Στη δυναμική, εισάγεται μια τέτοια έννοια ως "ιδανικό" μηχανικό σύστημα. Αυτό είναι ένα τέτοιο σύστημα, η παρουσία δεσμών στους οποίους δεν επηρεάζει την αλλαγή της κινητικής ενέργειας, δηλαδή

Τέτοιες συνδέσεις, που δεν αλλάζουν με την πάροδο του χρόνου και το άθροισμα της εργασίας τους στη στοιχειώδη μετατόπιση είναι ίσο με μηδέν, ονομάζονται ιδανικές και η εξίσωση (19.2.5) θα γραφεί:

Η δυναμική ενέργεια ενός υλικού σημείου σε μια δεδομένη θέση M ονομάζεται κλιμακωτή τιμή P, ίση με το έργο που θα παράγουν οι δυνάμεις πεδίου όταν το σημείο μετακινηθεί από τη θέση Μ στο μηδέν

P = A (mo) (19.3.1)

Η δυναμική ενέργεια εξαρτάται από τη θέση του σημείου Μ, δηλαδή από τις συντεταγμένες του

P = P (x, y, z) (19.3.2)

Ας εξηγήσουμε εδώ ότι το πεδίο δύναμης είναι μέρος του χωρικού όγκου, σε κάθε σημείο του οποίου μια δύναμη καθορισμένη σε μέγεθος και κατεύθυνση δρα στο σωματίδιο και εξαρτάται από τη θέση του σωματιδίου, δηλαδή από τις συντεταγμένες x, y. , z. Για παράδειγμα, το βαρυτικό πεδίο της Γης.

Η συνάρτηση U των συντεταγμένων, το διαφορικό της οποίας είναι ίσο με το έργο, ονομάζεται λειτουργία ισχύος... Το πεδίο δύναμης για το οποίο υπάρχει συνάρτηση δύναμης καλείται δυναμικό πεδίο, και οι δυνάμεις που δρουν σε αυτό το πεδίο είναι πιθανές δυνάμεις.

Έστω τα μηδενικά σημεία για δύο συναρτήσεις ισχύος (x, y, z) και U (x, y, z) να συμπίπτουν.

Με τον τύπο (14.3.5) λαμβάνουμε, δηλ. dA = dU (x, y, z) και

όπου U η τιμή της συνάρτησης δύναμης στο σημείο Μ. Ως εκ τούτου

П (x, y, z) = -U (x, y, z) (19.3.5)

Η δυναμική ενέργεια σε οποιοδήποτε σημείο του πεδίου δύναμης είναι ίση με την τιμή της συνάρτησης δύναμης σε αυτό το σημείο, λαμβανόμενη με το αντίθετο πρόσημο.

Δηλαδή, όταν εξετάζονται οι ιδιότητες ενός πεδίου δύναμης, αντί για συνάρτηση δύναμης, μπορεί κανείς να εξετάσει τη δυναμική ενέργεια και, ειδικότερα, η εξίσωση (19.3.3) θα ξαναγραφεί ως

Το έργο της δυναμικής δύναμης είναι ίσο με τη διαφορά στις τιμές της δυναμικής ενέργειας ενός κινούμενου σημείου στην αρχική και την τελική θέση.

Ειδικότερα, το έργο της βαρύτητας:

Αφήστε όλες τις δυνάμεις που δρουν στο σύστημα να είναι δυνητικές. Τότε, για κάθε σημείο k του συστήματος, το έργο ισούται με

Τότε για όλες τις δυνάμεις, εξωτερικές και εσωτερικές, θα υπάρχουν

όπου είναι η δυναμική ενέργεια ολόκληρου του συστήματος.

Αντικαθιστούμε αυτά τα αθροίσματα στην έκφραση για την κινητική ενέργεια (19.2.3):

ή τέλος:

Όταν κινούμαστε υπό την επίδραση δυνητικών δυνάμεων, το άθροισμα της κινητικής και δυναμικής ενέργειας του συστήματος σε κάθε θέση του παραμένει σταθερό. Αυτός είναι ο νόμος της διατήρησης της μηχανικής ενέργειας.

Ένα φορτίο βάρους 1 kg εκτελεί ελεύθερες δονήσεις σύμφωνα με το νόμο x = 0,1sinl0t. Συντελεστής ακαμψίας ελατηρίου c = 100 N / m. Προσδιορίστε τη συνολική μηχανική ενέργεια του φορτίου σε x = 0,05 m, εάν στο x = 0 η δυναμική ενέργεια είναι μηδέν . (0,5)

Ένα φορτίο με μάζα m = 4 kg, πέφτοντας προς τα κάτω, χρησιμοποιεί ένα νήμα για να περιστρέψει έναν κύλινδρο ακτίνας R = 0,4 m. Η ροπή αδράνειας του κυλίνδρου ως προς τον άξονα περιστροφής I = 0,2. Προσδιορίστε την κινητική ενέργεια του συστήματος των σωμάτων τη στιγμή που η ταχύτητα του φορτίου v = 2m / s . (10,5)

Ας ξεκινήσουμε με τον ορισμό. Εργασία ΕΝΑδύναμη φά κατά τη μετακίνηση NS το σώμα στο οποίο εφαρμόζεται ορίζεται ως το γινόμενο κουκίδων των διανυσμάτων φά και NS .

Α =F x = Fxcosα.(2.9.1)

Οπου α - η γωνία μεταξύ των κατευθύνσεων της δύναμης και της κίνησης.

Τώρα χρειαζόμαστε έκφραση (1.6 α), η οποία προκύπτει με ομοιόμορφα επιταχυνόμενη κίνηση. Θα βγάλουμε όμως ένα καθολικό συμπέρασμα, το οποίο ονομάζεται θεώρημα κινητικής ενέργειας. Ξαναγράφουμε λοιπόν την ισότητα (1.6 α)

ένα x=(V 2 –V 0 2)/2.

Πολλαπλασιάζουμε και τις δύο πλευρές της ισότητας με τη μάζα του σωματιδίου, παίρνουμε

Fx= m (V 2 –V 0 2) / 2.

Τελικά

A = m V 2/2 - Μ V 0 2/2. (2.9.1)

Η αξία μι=Μ V 2/2 ονομάζεται κινητική ενέργεια του σωματιδίου.

Έχετε συνηθίσει στο γεγονός ότι στη γεωμετρία τα θεωρήματα έχουν τη δική τους προφορική διατύπωση. Για να συμβαδίσουμε με αυτή την παράδοση, παρουσιάζουμε το θεώρημα της κινητικής ενέργειας σε μορφή κειμένου.

Η μεταβολή της κινητικής ενέργειας ενός σώματος είναι ίση με το έργο όλων των δυνάμεων που δρουν σε αυτό.

Αυτό το θεώρημα έχει καθολικό χαρακτήρα, ισχύει δηλαδή για κάθε τύπο κίνησης. Ωστόσο, η ακριβής απόδειξή του συνδέεται με τη χρήση ολοκληρωτικού λογισμού. Επομένως, το παραλείπουμε.

Εξετάστε ένα παράδειγμα κίνησης του σώματος σε ένα πεδίο βαρύτητας. Το έργο της βαρύτητας δεν εξαρτάται από τον τύπο της τροχιάς που συνδέει τα σημεία έναρξης και τέλους, αλλά καθορίζεται μόνο από τη διαφορά ύψους στις θέσεις έναρξης και λήξης:

A = mg ( η 1 –η 2). (2.9.2)

Ας πάρουμε ως αρχή κάποιο σημείο του πεδίου βαρύτητας και ας εξετάσουμε το έργο που γίνεται από τη βαρύτητα όταν ένα σωματίδιο μετακινείται σε αυτό το σημείο από ένα άλλο αυθαίρετο σημείο Rπου βρίσκεται σε ύψος η... Αυτή η εργασία ισούται με mghκαι ονομάζεται δυναμική ενέργεια μι n σωματίδια στο σημείο R:

μι n = mgh(2.9.3)

Τώρα μετασχηματίζουμε την ισότητα (2.9.1), το μηχανικό θεώρημα για την κινητική ενέργεια παίρνει τη μορφή

A = m V 2/2 - Μ V 0 2/2 = μι n1 - μι n2. (2.9.4)

Μ V 2/2 + μι n2 = Μ V 0 2/2 + μι n1.

Σε αυτή την ισότητα, στην αριστερή πλευρά υπάρχει το άθροισμα της κινητικής και της δυναμικής ενέργειας στο τελικό σημείο της τροχιάς και στη δεξιά πλευρά - στην αρχική.

Αυτή η ποσότητα ονομάζεται συνολική μηχανική ενέργεια. Θα το υποδηλώσουμε μι.

μι=μισε + μι NS.

Καταλήξαμε στο νόμο της διατήρησης της συνολικής ενέργειας: σε ένα κλειστό σύστημα, η συνολική ενέργεια διατηρείται.

Ωστόσο, πρέπει να γίνει μια παρατήρηση. Ενώ εξετάζαμε ένα παράδειγμα του λεγόμενου συντηρητικές δυνάμεις... Αυτές οι δυνάμεις εξαρτώνται μόνο από τη θέση στο χώρο. Και το έργο που γίνεται από τέτοιες δυνάμεις όταν μετακινείται ένα σώμα από τη μια θέση στην άλλη εξαρτάται μόνο από αυτές τις δύο θέσεις και δεν εξαρτάται από τη διαδρομή. Το έργο που επιτελείται από μια συντηρητική δύναμη είναι μηχανικά αναστρέψιμο, δηλαδή αλλάζει πρόσημο όταν το σώμα επανέλθει στην αρχική του θέση. Η βαρύτητα είναι μια συντηρητική δύναμη. Στο μέλλον, θα εξοικειωθούμε με άλλους τύπους συντηρητικών δυνάμεων, για παράδειγμα, με τη δύναμη της ηλεκτροστατικής αλληλεπίδρασης.

Στη φύση όμως υπάρχουν μη συντηρητικές δυνάμεις... Για παράδειγμα, δύναμη τριβής ολίσθησης. Όσο μεγαλύτερη είναι η διαδρομή του σωματιδίου, τόσο περισσότερη εργασία γίνεται από τη δύναμη τριβής ολίσθησης που ασκεί αυτό το σωματίδιο. Επιπλέον, το έργο της δύναμης τριβής ολίσθησης είναι πάντα αρνητικό, δηλαδή μια τέτοια δύναμη δεν μπορεί να «επιστρέψει» ενέργεια.

Για κλειστά συστήματα, η συνολική ενέργεια διατηρείται φυσικά. Αλλά για τις περισσότερες εργασίες στη μηχανική, είναι πιο σημαντικό ειδική περίπτωσηο νόμος της διατήρησης της ενέργειας, δηλαδή ο νόμος της διατήρησης της συνολικής μηχανικής ενέργειας. Ιδού η διατύπωσή του.

Εάν στο σώμα δρουν μόνο συντηρητικές δυνάμεις, τότε η συνολική μηχανική του ενέργεια, που ορίζεται ως το άθροισμα της κινητικής και της δυνητικής ενέργειας, διατηρείται.

Σε αυτό που ακολουθεί, χρειαζόμαστε δύο ακόμη σημαντικές ισότητες. Όπως πάντα, θα αντικαταστήσουμε το συμπέρασμα με μια απλή επίδειξη μιας συγκεκριμένης περίπτωσης του πεδίου βαρύτητας. Όμως η μορφή αυτών των ισοτήτων θα ισχύει για κάθε συντηρητική δύναμη.

Φέρνουμε την ισότητα (2.9.4) στη φόρμα

A = F∆x = Ε n1 - μι n2 = - ( μι n.con - μια.σ.) = - ∆U.

Εδώ εξετάσαμε το έργο ΕΝΑόταν το σώμα κινείται απόσταση Δ Χ.Η τιμή ΔU, ίση με τη διαφορά μεταξύ της τελικής και της αρχικής δυναμικής ενέργειας, ονομάζεται μεταβολή της δυναμικής ενέργειας. Και η ισότητα που προκύπτει αξίζει μια ξεχωριστή γραμμή και έναν ειδικό αριθμό. Ας σπεύσουμε να του το αναθέσουμε:

Α =- ∆U (2.9.5)

Αυτό συνεπάγεται επίσης μια μαθηματική σχέση μεταξύ δύναμης και δυναμικής ενέργειας:

φά= - ∆U / ∆ Χ(2.9.6)

Στη γενική περίπτωση, που δεν σχετίζεται με το πεδίο βαρύτητας, η ισότητα (2.9.6) είναι η απλούστερη διαφορική εξίσωση

F = - dU / dx.

Ας εξετάσουμε το τελευταίο παράδειγμα χωρίς απόδειξη. Η βαρυτική δύναμη περιγράφεται από το νόμο της βαρύτητας F (r) = GmM / r 2και είναι συντηρητικός. Η έκφραση για τη δυναμική ενέργεια του βαρυτικού πεδίου είναι:

U (r) = –GmM / r.

συγγραφέας: – Ας δούμε μια απλή περίπτωση. Σε ένα σώμα μάζας το m, που βρίσκεται σε οριζόντιο επίπεδο, δρα για μια χρονική περίοδο Τοριζόντια δύναμη φά... Δεν υπάρχει τριβή. Τι είναι το έργο της δύναμης φά?

Μαθητης σχολειου: – Στη διάρκεια Ττο σώμα θα κινηθεί σε απόσταση S = στο 2/2, όπου ένα=φά/ Μ. Επομένως, το αναζητούμενο έργο είναι ΕΝΑ=φά S = φά 2 Τ 2 / (2μ).

συγγραφέας: Όλα είναι σωστά αν υποθέσουμε ότι το σώμα βρισκόταν σε ηρεμία πριν αρχίσει να ενεργεί η δύναμη πάνω του. Ας περιπλέκουμε λίγο το έργο. Αφήστε το σώμα να κινηθεί ευθύγραμμα και ομοιόμορφα με μια ορισμένη ταχύτητα V 0, συν-κατευθυνόμενη με την εξωτερική δύναμη, πριν αρχίσει να ενεργεί η δύναμη. Ποια είναι η εργασία ανά χρόνο τώρα Τ?

Μαθητης σχολειου: – Για να υπολογίσω τη μετατόπιση, θα πάρω έναν γενικότερο τύπο S = V 0 Τ+στο 2/2, για δουλειά παίρνω ΕΝΑ=φά(V 0 Τ+στο 2/2). Σε σύγκριση με το προηγούμενο αποτέλεσμα, βλέπω ότι η ίδια δύναμη παράγει διαφορετικό έργο για τις ίδιες χρονικές περιόδους.

Ένα σώμα μάζας m ολισθαίνει σε κεκλιμένο επίπεδο με γωνία κλίσης α. Ο συντελεστής τριβής ολίσθησης του σώματος έναντι του επιπέδου κ... Μια οριζόντια δύναμη δρα στο σώμα όλη την ώρα. φά... Ποιο είναι το έργο αυτής της δύναμης όταν το σώμα κινείται σε απόσταση S;

Μαθητης σχολειου: – Ας κάνουμε την ευθυγράμμιση των δυνάμεων και ας βρούμε το αποτέλεσμά τους. Μια εξωτερική δύναμη F δρα στο σώμα, καθώς και η βαρύτητα, η αντίδραση υποστήριξης και η τριβή.

Μαθητης σχολειου: – Αποδεικνύεται ότι το έργο A = φάμικρό συνα και τέλος. Πραγματικά με απογοήτευσε η συνήθεια να ψάχνω όλες τις δυνάμεις κάθε φορά, ειδικά επειδή το πρόβλημα δείχνει τη μάζα και τον συντελεστή τριβής.

Μαθητης σχολειου: – Έργο δύναμης φάΈχω ήδη υπολογίσει: A 1 = φάμικρό συνα. Το έργο της βαρύτητας είναι A 2 = mgS αμαρτίαα. Το έργο της δύναμης τριβής ... είναι αρνητικό, αφού τα διανύσματα δύναμης και μετατόπισης είναι αντίθετα κατευθυνόμενα: А 3 = - kmgS συνα. Το έργο της δύναμης αντίδρασης Νείναι μηδέν γιατί η δύναμη και η μετατόπιση είναι κάθετες. Αλήθεια, δεν καταλαβαίνω πραγματικά την έννοια της αρνητικής δουλειάς;

συγγραφέας: – Αυτό σημαίνει ότι το έργο αυτής της δύναμης μειώνει την κινητική ενέργεια του σώματος. Παρεμπιπτόντως. Ας συζητήσουμε την κίνηση του σώματος που φαίνεται στο σχήμα 2.9.1 από την άποψη του νόμου της διατήρησης της ενέργειας. Πρώτα, βρείτε το συνολικό έργο όλων των δυνάμεων.

Μαθητης σχολειου: - ΕΝΑ= ΕΝΑ 1 + ΕΝΑ 2 + ΕΝΑ 3 = FS συνα + mgS αμαρτίαα– kmgS συνα.

Σύμφωνα με το θεώρημα της κινητικής ενέργειας, η διαφορά μεταξύ της κινητικής ενέργειας στην τελική και αρχική κατάσταση είναι ίση με το έργο που γίνεται στο σώμα:

μιΠρος το - μι n = ΕΝΑ.

Μαθητης σχολειου: – Θα μπορούσε να είναι ότι αυτές ήταν άλλες εξισώσεις που δεν σχετίζονται με αυτό το πρόβλημα;

συγγραφέας: – Αλλά όλες οι εξισώσεις πρέπει να δίνουν το ίδιο αποτέλεσμα. Το θέμα είναι ότι η δυναμική ενέργεια περιέχεται σε λανθάνουσα μορφή στην έκφραση για πλήρη εργασία. Πράγματι, θυμηθείτε A 2 = mgS αμαρτίαα = mgh, όπου h είναι το ύψος της καθόδου του σώματος. Πάρτε, τώρα από το θεώρημα της κινητικής ενέργειας, την έκφραση του νόμου της διατήρησης της ενέργειας.

Μαθητης σχολειου: – Εφόσον mgh = U n - U k, όπου U n και U k είναι η αρχική και η τελική δυνητική ενέργεια του σώματος, αντίστοιχα, έχουμε:

Μ V n 2/2 + U n + ΕΝΑ 1 + ΕΝΑ 3 = m Vέως 2/2 + UΠρος το.

Μαθητης σχολειου: – Αυτό, κατά τη γνώμη μου, είναι εύκολο. Το έργο της δύναμης τριβής σε μέτρο είναι ακριβώς ίσο με την ποσότητα της θερμότητας Q... Να γιατί Q= kmgS συνα.

Μαθητης σχολειου: Μ V n 2/2 + U n + ΕΝΑ 1 – Q= m Vέως 2/2 + UΠρος το.

συγγραφέας: – Τώρα ας γενικεύσουμε λίγο τον ορισμό της εργασίας. Το θέμα είναι ότι η σχέση (2.9.1) ισχύει μόνο για την περίπτωση σταθερής δύναμης. Αν και υπάρχουν πολλές περιπτώσεις που η ίδια η δύναμη εξαρτάται από την κίνηση του σωματιδίου. Δώσε ένα παράδειγμα.

Μαθητης σχολειου: – Το πρώτο πράγμα που έρχεται στο μυαλό είναι το τέντωμα του ελατηρίου. Καθώς το μη ασφαλισμένο άκρο του ελατηρίου κινείται, η δύναμη αυξάνεται. Το δεύτερο παράδειγμα συνδέεται με ένα εκκρεμές, το οποίο, όπως γνωρίζουμε, είναι πιο δύσκολο να συγκρατηθεί σε μεγάλες αποκλίσεις από τη θέση ισορροπίας.

συγγραφέας: – Καλός. Ας πάρουμε ένα παράδειγμα με ένα ελατήριο. Η ελαστική δύναμη ενός ιδανικού ελατηρίου περιγράφεται από το νόμο του Hooke, σύμφωνα με τον οποίο, όταν το ελατήριο συμπιέζεται (ή τεντώνεται) κατά ένα NSπροκύπτει μια δύναμη αντίθετη από τη μετατόπιση, γραμμικά εξαρτώμενη από NS... Ας γράψουμε τον νόμο του Χουκ με τη μορφή ισότητας:

φά= - k Χ (2.9.2)

Εδώ k είναι ο συντελεστής ακαμψίας του ελατηρίου, Χ- το μέγεθος της παραμόρφωσης του ελατηρίου. Σχεδιάστε ένα γράφημα εξάρτησης φά(Χ).

Μαθητης σχολειου: Το σχέδιό μου φαίνεται στην εικόνα.

Εικ. 2.9.2

Το αριστερό μισό του γραφήματος αντιστοιχεί σε συμπίεση ελατηρίου και το δεξί μισό σε τάση.

συγγραφέας: – Τώρα ας υπολογίσουμε το έργο της δύναμης F όταν μετακινούμαστε από NS= 0 έως NS= S. Υπάρχει ένας γενικός κανόνας για αυτό. Εάν γνωρίζουμε τη γενική εξάρτηση της δύναμης από τη μετατόπιση, τότε το έργο στην τομή από x 1 έως x 2 είναι η περιοχή κάτω από την καμπύλη F (x) σε αυτό το τμήμα.

Μαθητης σχολειου: – Αυτό σημαίνει ότι το έργο της ελαστικής δύναμης όταν το σώμα κινείται από NS= 0 έως NS= Το S είναι αρνητικό και το μέτρο του είναι ίσο με το εμβαδόν ενός ορθογώνιου τριγώνου: ΕΝΑ= kS 2/2.

ΕΝΑ= κ NS 2 /2. (2.9.3)

Αυτό το έργο μετατρέπεται σε δυναμική ενέργεια του παραμορφωμένου ελατηρίου.

Ιστορία.

Ο Ράδερφορντ έδειξε τη διάσπαση του ραδίου στο κοινό. Η οθόνη έλαμψε και σκοτείνιασε.

– Τώρα βλέπεις – είπε ο Ράδερφορντ, – ότι τίποτα δεν φαίνεται. Και γιατί δεν μπορείτε να δείτε τίποτα, θα το δείτε τώρα.

Ρυθμίστε τις τιμές σωματικού βάρους χρησιμοποιώντας τα ρυθμιστικάΜ, η γωνία κλίσης του επιπέδουένα, εξωτερική δύναμη ΣΤ εσωτ , συντελεστής τριβήςΜκαι επιτάχυνση ένααναφέρονται στον Πίνακα 1 για την ομάδα σας.

Ενεργοποιήστε ταυτόχρονα το χρονόμετρο και πατήστε το κουμπί "Έναρξη". Απενεργοποιήστε το χρονόμετρο όταν το σώμα σταματήσει στο τέλος του κεκλιμένου επιπέδου.

Επαναλάβετε αυτό το πείραμα 10 φορές και καταγράψτε τα αποτελέσματα της μέτρησης του χρόνου ολίσθησης του σώματος από ένα κεκλιμένο επίπεδο στον πίνακα. 2.

ΠΙΝΑΚΑΣ 1. Αρχικές παράμετροι του πειράματος

Ταξίαρχος Αρ.
m, kg
Μ	0,10
α, βαθ
F int, Ν
α, m/s 2

ΠΙΝΑΚΑΣ 2. Αποτελέσματα μετρήσεων και υπολογισμών

W p = - δυναμική ενέργεια του σώματος στο πάνω σημείο του κεκλιμένου επιπέδου.

Δ) - το έργο της δύναμης τριβής στο τμήμα καθόδου.

ΜΙ) - το έργο μιας εξωτερικής δύναμης στο τμήμα καθόδου

και γράψτε αυτές τις τιμές στις αντίστοιχες γραμμές του πίνακα. 2. Υπολογίστε τις μέσες τιμές αυτών των παραμέτρων και σημειώστε τις στη στήλη «μέσες τιμές» του Πίνακα 2.

Χρησιμοποιώντας τον τύπο (7), ελέγξτε την εκπλήρωση του νόμου της διατήρησης της μηχανικής ενέργειας όταν ένα σώμα κινείται κατά μήκος ενός κεκλιμένου επιπέδου. Υπολογίστε τα λάθη και βγάλτε συμπεράσματα με βάση τα αποτελέσματα των πειραμάτων.

Ερωτήσεις και εργασίες για αυτοέλεγχο

1. Ποιος είναι ο νόμος διατήρησης της μηχανικής ενέργειας;

2. Για ποια συστήματα πληρούται ο νόμος διατήρησης της μηχανικής ενέργειας;

3. Ποια είναι η διαφορά μεταξύ ενέργειας και εργασίας;

4. Ποιος είναι ο λόγος της αλλαγής της δυνητικής ενέργειας;

5. Ποιος ο λόγος της αλλαγής της κινητικής ενέργειας;

6. Είναι απαραίτητο να πληρούται η προϋπόθεση της κλειστότητας του μηχανικού συστήματος των σωμάτων για να εκπληρωθεί ο νόμος διατήρησης της μηχανικής ενέργειας;

7. Ποιες δυνάμεις ονομάζονται συντηρητικές;

8. Ποιες δυνάμεις ονομάζονται διαλυτικές;

9. Το σώμα τραβιέται αργά στον λόφο. Εξαρτήστε τα ακόλουθα από το σχήμα του προφίλ του βουνού: α) το έργο της δύναμης της βαρύτητας; β) το έργο της δύναμης τριβής; Τα σημεία έναρξης και λήξης της κίνησης του σώματος είναι σταθερά.

10. Το σώμα γλιστράει από την κορυφή του κεκλιμένου επιπέδου χωρίς αρχική ταχύτητα. Εξαρτάται το έργο της δύναμης τριβής σε όλη τη διαδρομή κίνησης του σώματος έως το στοπ στο οριζόντιο τμήμα: α) από τη γωνία κλίσης του επιπέδου; β) στον συντελεστή τριβής;

11. Σε κεκλιμένο επίπεδο, δύο σώματα γλιστρούν από το ίδιο ύψος: ένα με μάζαΜ , ένα άλλο με μάζα 2Μ ... Ποιο από τα σώματα θα διανύσει τη μεγαλύτερη απόσταση κατά μήκος του οριζόντιου τμήματος μέχρι τη στάση και πόσες φορές; Οι συντελεστές τριβής και για τα δύο σώματα είναι ίδιοι.

12.Έλκηθρα μάζας m κατέβηκε από ένα βουνό ύψους Η και σταμάτησε σε οριζόντιο τμήμα. Τι δουλειά πρέπει να γίνει για να ανέβουν στο βουνό κατά μήκος της κυλιόμενης γραμμής.

13. Με την ίδια αρχική ταχύτητα, το σώμα περνά από: α) μια κατάθλιψη. β) μια ολίσθηση που έχει τα ίδια τόξα τροχιάς και τους ίδιους συντελεστές τριβής. Συγκρίνετε τις ταχύτητες του σώματος στο τέλος της διαδρομής και στις δύο περιπτώσεις.

Λογοτεχνία

1. Trofimova T.I. μάθημα φυσικής. Κεφ. 3, §§12,13.

Αρ.

Ο μέσος όρος έννοια

Ταφή

t, s

v, m / s

S, m

W k, J

W p, J

A tr, J

A int, J

W full, J

Θέα:αυτό το άρθρο έχει διαβαστεί 48440 φορές

Pdf Επιλογή γλώσσας ... Ρωσικά Ουκρανικά Αγγλικά

Σύντομη κριτική

Ολόκληρο το υλικό κατεβάζεται παραπάνω, έχοντας προηγουμένως επιλέξει τη γλώσσα

Δύο περιπτώσεις μετασχηματισμού της μηχανικής κίνησης ενός υλικού σημείου ή ενός συστήματος σημείων:

1. Η μηχανική κίνηση μεταφέρεται από το ένα μηχανικό σύστημα στο άλλο ως μηχανική κίνηση.
2. η μηχανική κίνηση μετατρέπεται σε άλλη μορφή κίνησης της ύλης (με τη μορφή δυναμικής ενέργειας, θερμότητας, ηλεκτρισμού κ.λπ.).

Όταν ο μετασχηματισμός της μηχανικής κίνησης θεωρείται χωρίς τη μετάβασή της σε άλλη μορφή κίνησης, το μέτρο της μηχανικής κίνησης είναι το διάνυσμα της ορμής ενός υλικού σημείου ή ενός μηχανικού συστήματος. Το μέτρο της δράσης της δύναμης σε αυτή την περίπτωση είναι το διάνυσμα της ώθησης της δύναμης.

Όταν η μηχανική κίνηση μετατρέπεται σε άλλη μορφή κίνησης της ύλης, η κινητική ενέργεια ενός υλικού σημείου ή ενός μηχανικού συστήματος λειτουργεί ως μέτρο της μηχανικής κίνησης. Το μέτρο της δράσης της δύναμης όταν μια μηχανική κίνηση μετατρέπεται σε άλλη μορφή κίνησης είναι το έργο της δύναμης

Κινητική ενέργεια

Η κινητική ενέργεια είναι η ικανότητα του σώματος να ξεπερνά τα εμπόδια ενώ κινείται.

Κινητική ενέργεια υλικού σημείου

Η κινητική ενέργεια ενός υλικού σημείου είναι μια κλιμακωτή ποσότητα που ισούται με το μισό γινόμενο της μάζας του σημείου επί το τετράγωνο της ταχύτητάς του.

Κινητική ενέργεια:

• χαρακτηρίζει τόσο τις μεταφορικές όσο και τις περιστροφικές κινήσεις.
• δεν εξαρτάται από την κατεύθυνση κίνησης των σημείων του συστήματος και δεν χαρακτηρίζει την αλλαγή σε αυτές τις κατευθύνσεις.
• χαρακτηρίζει τη δράση τόσο εσωτερικών όσο και εξωτερικών δυνάμεων.

Κινητική ενέργεια μηχανικού συστήματος

Η κινητική ενέργεια του συστήματος είναι ίση με το άθροισμα των κινητικών ενεργειών των σωμάτων του συστήματος. Η κινητική ενέργεια εξαρτάται από το είδος της κίνησης των σωμάτων του συστήματος.

Προσδιορισμός της κινητικής ενέργειας ενός στερεού στο ΔΙΑΦΟΡΕΤΙΚΟΙ ΤΥΠΟΙκινήσεις κινήσεις.

Κινητική ενέργεια μεταφορικής κίνησης
Στη μεταφορική κίνηση, η κινητική ενέργεια του σώματος είναι Τ=Μ V 2/2.

Η μάζα είναι ένα μέτρο της αδράνειας του σώματος κατά τη μεταφορική κίνηση.

Κινητική ενέργεια της περιστροφικής κίνησης του σώματος

Κατά την περιστροφική κίνηση του σώματος, η κινητική ενέργεια ισούται με το μισό του γινόμενου της ροπής αδράνειας του σώματος σε σχέση με τον άξονα περιστροφής και το τετράγωνο της γωνιακής του ταχύτητας.

Το μέτρο της αδράνειας ενός σώματος κατά την περιστροφική κίνηση είναι η ροπή αδράνειας.

Η κινητική ενέργεια ενός σώματος δεν εξαρτάται από την φορά περιστροφής του σώματος.

Κινητική ενέργεια κίνησης επιπέδου-παράλληλης σώματος

Με την επίπεδη-παράλληλη κίνηση του σώματος, η κινητική ενέργεια ισούται με

Έργο δύναμης

Το έργο της δύναμης χαρακτηρίζει τη δράση της δύναμης στο σώμα σε κάποια μετατόπιση και καθορίζει τη μεταβολή του συντελεστή της ταχύτητας του κινούμενου σημείου.

Στοιχειώδες έργο δύναμης

Το στοιχειώδες έργο της δύναμης ορίζεται ως μια κλιμακωτή ποσότητα ίση με το γινόμενο της προβολής της δύναμης από την εφαπτομένη στην τροχιά, που κατευθύνεται προς την κατεύθυνση κίνησης του σημείου, και την απειροελάχιστη μετατόπιση του σημείου, που κατευθύνεται κατά μήκος αυτού εφαπτομένος.

Αναγκαστική εργασία στην τελική μετατόπιση

Το έργο της δύναμης στην τελική μετατόπιση είναι ίσο με το άθροισμα του έργου της σε στοιχειώδη τμήματα.

Το έργο της δύναμης στην τελική μετατόπιση M 1 M 0 είναι ίσο με το ολοκλήρωμα κατά μήκος αυτής της μετατόπισης από το στοιχειώδες έργο.

Το έργο της δύναμης στη μετατόπιση M 1 M 2 απεικονίζεται από την περιοχή του σχήματος που οριοθετείται από τον άξονα της τετμημένης, την καμπύλη και τις τεταγμένες που αντιστοιχούν στα σημεία M 1 και M 0.

Η μονάδα μέτρησης του εργατικού δυναμικού και της κινητικής ενέργειας σε SI 1 (J).

Θεωρήματα εργασίας δυνάμεων

Θεώρημα 1... Το έργο της προκύπτουσας δύναμης σε μια ορισμένη μετατόπιση είναι ίσο με το αλγεβρικό άθροισμα του έργου των συνισταμένων δυνάμεων στην ίδια μετατόπιση.

Θεώρημα 2.Το έργο μιας σταθερής δύναμης στην προκύπτουσα μετατόπιση είναι ίσο με το αλγεβρικό άθροισμα του έργου αυτής της δύναμης στις μετατοπίσεις των συνιστωσών.

Εξουσία

Η ισχύς είναι ένα μέγεθος που καθορίζει το έργο της δύναμης ανά μονάδα χρόνου.

Η μονάδα μέτρησης ισχύος είναι 1W = 1 J / s.

Περιπτώσεις προσδιορισμού του έργου των δυνάμεων

Έργο εσωτερικών δυνάμεων

Το άθροισμα του έργου των εσωτερικών δυνάμεων ενός άκαμπτου σώματος σε οποιαδήποτε μετατόπισή του είναι ίσο με μηδέν.

Έργο βαρύτητας

Εργασία ελαστικής δύναμης

Εργασία δύναμης τριβής

Το έργο των δυνάμεων που ασκούνται σε ένα περιστρεφόμενο σώμα

Το στοιχειώδες έργο των δυνάμεων που ασκούνται σε ένα άκαμπτο σώμα που περιστρέφεται γύρω από έναν σταθερό άξονα είναι ίσο με το γινόμενο της κύριας ροπής των εξωτερικών δυνάμεων σε σχέση με τον άξονα περιστροφής κατά την αύξηση της γωνίας περιστροφής.

Αντίσταση κύλισης

Στη ζώνη επαφής του ακίνητου κυλίνδρου και του επιπέδου, εμφανίζεται μια τοπική παραμόρφωση της συμπίεσης επαφής, η τάση κατανέμεται σύμφωνα με έναν ελλειπτικό νόμο και η γραμμή δράσης του προκύπτοντος N αυτών των τάσεων συμπίπτει με τη γραμμή δράσης του φορτίου δύναμη στον κύλινδρο Q. Όταν ο κύλινδρος κυλά, η κατανομή του φορτίου γίνεται ασύμμετρη με το μέγιστο να μετατοπίζεται προς την κατεύθυνση της κίνησης. Το προκύπτον N μετατοπίζεται από την τιμή k - ο βραχίονας της δύναμης τριβής κύλισης, ο οποίος ονομάζεται επίσης συντελεστής τριβής κύλισης και έχει τη διάσταση του μήκους (cm)

Το θεώρημα για τη μεταβολή της κινητικής ενέργειας ενός υλικού σημείου

Η μεταβολή της κινητικής ενέργειας ενός υλικού σημείου σε κάποια μετατόπισή του είναι ίση με το αλγεβρικό άθροισμα του ρομπότ όλων των δυνάμεων που δρουν στο σημείο με την ίδια μετατόπιση.

Το θεώρημα για τη μεταβολή της κινητικής ενέργειας ενός μηχανικού συστήματος

Η μεταβολή της κινητικής ενέργειας ενός μηχανικού συστήματος σε μια ορισμένη μετατόπιση είναι ίση με το αλγεβρικό άθροισμα των εσωτερικών και εξωτερικών δυνάμεων του ρομπότ που δρουν στα υλικά σημεία του συστήματος με την ίδια μετατόπιση.

Το θεώρημα για τη μεταβολή της κινητικής ενέργειας ενός άκαμπτου σώματος

Η μεταβολή της κινητικής ενέργειας ενός άκαμπτου σώματος (αμετάβλητο σύστημα) σε μια ορισμένη μετατόπιση είναι ίση με το άθροισμα των εξωτερικών δυνάμεων του ρομπότ που δρουν στα σημεία του συστήματος με την ίδια μετατόπιση.

Αποδοτικότητα

Δυνάμεις που δρουν σε μηχανισμούς

Οι δυνάμεις και τα ζεύγη δυνάμεων (στιγμών) που εφαρμόζονται σε έναν μηχανισμό ή μια μηχανή μπορούν να χωριστούν σε ομάδες:

1. Κινητήριες δυνάμεις και ροπές που εκτελούν θετικό έργο (που εφαρμόζεται στους κινητήριους συνδέσμους, για παράδειγμα, πίεση αερίου σε έμβολο σε κινητήρα εσωτερικής καύσης).

2. Δυνάμεις και ροπές αντίστασης που εκτελούν αρνητικό έργο:

• χρήσιμη αντίσταση (εκτελούν την εργασία που απαιτείται από το μηχάνημα και εφαρμόζονται στους κινητήριους συνδέσμους, για παράδειγμα, η αντίσταση του φορτίου που ανυψώνεται από το μηχάνημα),
• δυνάμεις αντίστασης (για παράδειγμα, δυνάμεις τριβής, αντίσταση αέρα κ.λπ.).

3. Οι δυνάμεις της βαρύτητας και οι δυνάμεις ελαστικότητας των ελατηρίων (τόσο θετικό όσο και αρνητικό έργο, ενώ το έργο για έναν πλήρη κύκλο είναι ίσο με μηδέν).

4. Δυνάμεις και ροπές που εφαρμόζονται στο σώμα ή στο ράφι από έξω (αντίδραση του θεμελίου κ.λπ.), οι οποίες δεν εκτελούν έργο.

5. Δυνάμεις αλληλεπίδρασης μεταξύ συνδέσμων, που δρουν σε κινηματικά ζεύγη.

6. Οι δυνάμεις αδράνειας των συνδέσμων, που προκαλούνται από τη μάζα και την κίνηση των συνδέσμων με επιτάχυνση, μπορούν να εκτελέσουν θετικό, αρνητικό έργο και να μην κάνουν έργο.

Έργο δυνάμεων σε μηχανισμούς

Στη σταθερή κατάσταση λειτουργίας του μηχανήματος, η κινητική του ενέργεια δεν μεταβάλλεται και το άθροισμα του έργου των κινητήριων δυνάμεων και των δυνάμεων αντίστασης που εφαρμόζονται σε αυτό είναι ίσο με μηδέν.

Η εργασία που δαπανάται για να τεθεί το μηχάνημα σε κίνηση δαπανάται για να ξεπεραστούν χρήσιμες και επιβλαβείς αντιστάσεις.

Αποτελεσματικότητα μηχανισμών

Η μηχανική απόδοση σε σταθερή κίνηση είναι ίση με την αναλογία χρήσιμη εργασίαμηχάνημα στην εργασία που δαπανήθηκε για τη θέση του μηχανήματος σε κίνηση:

Τα στοιχεία της μηχανής μπορούν να συνδεθούν σε σειρά, παράλληλα και μεικτά.

Αποδοτικότητα σε σύνδεση σε σειρά

Με μια σειρά σύνδεσης μηχανισμών, η συνολική απόδοση είναι μικρότερη με τη χαμηλότερη απόδοση ενός μεμονωμένου μηχανισμού.

Αποδοτικότητα με παράλληλη σύνδεση

Με την παράλληλη σύνδεση μηχανισμών, η συνολική απόδοση είναι μεγαλύτερη από τη χαμηλότερη και μικρότερη από την υψηλότερη απόδοση ενός μεμονωμένου μηχανισμού.

Μορφή: pdf

Γλώσσα: Ρωσικά, Ουκρανικά

Ένα παράδειγμα υπολογισμού ενός γραναζιού στροφείου
Ένα παράδειγμα υπολογισμού ενός γραναζιού στροφείου. Έγινε η επιλογή του υλικού, ο υπολογισμός των επιτρεπόμενων τάσεων, ο υπολογισμός της επαφής και της αντοχής σε κάμψη.

Ένα παράδειγμα επίλυσης του προβλήματος της κάμψης μιας δοκού
Στο παράδειγμα, κατασκευάζονται διαγράμματα δυνάμεων διάτμησης και ροπών κάμψης, εντοπίζεται επικίνδυνη τομή και επιλέγεται μια δέσμη Ι. Το πρόβλημα αναλύει την κατασκευή διαγραμμάτων χρησιμοποιώντας διαφορικές εξαρτήσεις, πραγματοποιείται συγκριτική ανάλυση διαφόρων διατομών της δοκού.

Ένα παράδειγμα επίλυσης του προβλήματος της στρέψης του άξονα
Ο στόχος είναι να ελέγξετε την αντοχή ενός χαλύβδινου άξονα για δεδομένη διάμετρο, υλικό και επιτρεπόμενες τάσεις. Κατά τη διάρκεια της λύσης, σχεδιάζονται διαγράμματα ροπών, διατμητικές τάσεις και γωνίες στρέψης. Το νεκρό βάρος του άξονα δεν λαμβάνεται υπόψη.

Ένα παράδειγμα επίλυσης του προβλήματος τάσης-συμπίεσης μιας ράβδου
Ο στόχος είναι να ελέγξετε την αντοχή μιας χαλύβδινης ράβδου σε μια δεδομένη επιτρεπόμενη τάση. Στην πορεία της λύσης, σχεδιάζονται διαγράμματα διαμήκων δυνάμεων, κανονικών τάσεων και μετατοπίσεων. Το βάρος της ράβδου δεν λαμβάνεται υπόψη.

Εφαρμογή του θεωρήματος διατήρησης της κινητικής ενέργειας
Ένα παράδειγμα επίλυσης του προβλήματος σχετικά με την εφαρμογή του θεωρήματος για τη διατήρηση της κινητικής ενέργειας ενός μηχανικού συστήματος

Ενέργειαονομάζεται κλιμακωτό φυσικό μέγεθος, το οποίο είναι ένα ενιαίο μέτρο των διαφόρων μορφών κίνησης της ύλης και ένα μέτρο της μετάβασης της κίνησης της ύλης από τη μια μορφή στην άλλη.

Για να χαρακτηριστούν οι διάφορες μορφές κίνησης της ύλης, εισάγονται κατάλληλοι τύποι ενέργειας, για παράδειγμα: μηχανικές, εσωτερικές, ενέργεια ηλεκτροστατικών, ενδοπυρηνικών αλληλεπιδράσεων κ.λπ.

Η ενέργεια υπακούει στο νόμο διατήρησης, που είναι ένας από τους πιο σημαντικούς νόμους της φύσης.

Η μηχανική ενέργεια Ε χαρακτηρίζει την κίνηση και την αλληλεπίδραση των σωμάτων και είναι συνάρτηση των ταχυτήτων και της αμοιβαίας διάταξης των σωμάτων. Είναι ίσο με το άθροισμα της κινητικής και της δυνητικής ενέργειας.

Κινητική ενέργεια

Σκεφτείτε την περίπτωση όταν ένα σώμα με μάζα Μυπάρχει μια σταθερή δύναμη \ (~ \ vec F \) (μπορεί να είναι το αποτέλεσμα πολλών δυνάμεων) και τα διανύσματα δύναμης \ (~ \ vec F \) και οι μετατοπίσεις \ (~ \ vec s \) κατευθύνονται κατά μήκος μιας ευθείας γραμμή προς μία κατεύθυνση. Σε αυτή την περίπτωση, το έργο της δύναμης μπορεί να οριστεί ως ΕΝΑ = φά∙μικρό... Το μέτρο δύναμης σύμφωνα με τον δεύτερο νόμο του Νεύτωνα είναι φά = m ∙ aκαι τη μονάδα μετατόπισης μικρόμε ομοιόμορφα επιταχυνόμενη ευθύγραμμη κίνηση, συνδέεται με τις μονάδες του αρχικού υ 1 και τελικό υ 2 ταχύτητες και επιταχύνσεις έναέκφραση \ (~ s = \ frac (\ upsilon ^ 2_2 - \ upsilon ^ 2_1) (2a) \).

Από εδώ, για δουλειά, παίρνουμε

\ (~ A = F \ cdot s = m \ cdot a \ cdot \ frac (\ upsilon ^ 2_2 - \ upsilon ^ 2_1) (2a) = \ frac (m \ cdot \ upsilon ^ 2_2) (2) - \ frac (m \ cdot \ upsilon ^ 2_1) (2) \). (1)

Φυσικό μέγεθος ίσο με το μισό γινόμενο της μάζας ενός σώματος με το τετράγωνο της ταχύτητάς του λέγεται κινητική ενέργεια του σώματος.

Η κινητική ενέργεια συμβολίζεται με το γράμμα μικ.

\ (~ E_k = \ frac (m \ cdot \ upsilon ^ 2) (2) \). (2)

Τότε η ισότητα (1) μπορεί να γραφτεί ως εξής:

\ (~ A = E_ (k2) - E_ (k1) \). (3)

Θεώρημα κινητικής ενέργειας

το έργο των δυνάμεων που προκύπτουν που ασκούνται στο σώμα είναι ίσο με τη μεταβολή της κινητικής ενέργειας του σώματος.

Εφόσον η μεταβολή της κινητικής ενέργειας είναι ίση με το έργο της δύναμης (3), η κινητική ενέργεια του σώματος εκφράζεται στις ίδιες μονάδες με το έργο, δηλαδή σε τζάουλ.

Αν η αρχική ταχύτητα κίνησης ενός σώματος με μάζα Μισούται με μηδέν και το σώμα αυξάνει την ταχύτητά του στην τιμή υ , τότε το έργο της δύναμης είναι ίσο με την τελική τιμή της κινητικής ενέργειας του σώματος:

\ (~ A = E_ (k2) - E_ (k1) = \ frac (m \ cdot \ upsilon ^ 2) (2) - 0 = \ frac (m \ cdot \ upsilon ^ 2) (2) \). (4)

Η φυσική έννοια της κινητικής ενέργειας

η κινητική ενέργεια ενός σώματος που κινείται με ταχύτητα υ δείχνει τι δουλειά πρέπει να κάνει μια δύναμη που ασκεί σε ένα σώμα σε ηρεμία για να του προσδώσει αυτή την ταχύτητα.

Δυναμική ενέργεια

Δυναμική ενέργειαΕίναι η ενέργεια της αλληλεπίδρασης των σωμάτων.

Η δυναμική ενέργεια ενός σώματος που υψώνεται πάνω από τη Γη είναι η ενέργεια της αλληλεπίδρασης μεταξύ του σώματος και της Γης μέσω βαρυτικών δυνάμεων. Η δυναμική ενέργεια ενός ελαστικά παραμορφωμένου σώματος είναι η ενέργεια αλληλεπίδρασης μεμονωμένων τμημάτων του σώματος μεταξύ τους με ελαστικές δυνάμεις.

Δυνητικόςλέγονται δύναμη, του οποίου το έργο εξαρτάται μόνο από την αρχική και τελική θέση ενός κινούμενου υλικού σημείου ή σώματος και δεν εξαρτάται από το σχήμα της τροχιάς.

Με μια κλειστή τροχιά, το έργο της δυνητικής δύναμης είναι πάντα μηδέν. Οι δυνάμει δυνάμεις περιλαμβάνουν βαρυτικές δυνάμεις, ελαστικές δυνάμεις, ηλεκτροστατικές δυνάμεις και μερικές άλλες.

Δυνάμειςτων οποίων το έργο εξαρτάται από το σχήμα της τροχιάς ονομάζονται μη δυναμικό... Όταν ένα υλικό σημείο ή σώμα κινείται κατά μήκος μιας κλειστής τροχιάς, το έργο της μη δυνητικής δύναμης δεν είναι μηδέν.

Δυνητική ενέργεια αλληλεπίδρασης του σώματος με τη Γη

Εύρεση του έργου που γίνεται από τη βαρύτητα φά t όταν κινείται ένα σώμα με μάζα Μκατακόρυφα κάτω από ύψος η 1 πάνω από την επιφάνεια της Γης σε ύψος η 2 (εικ. 1). Αν η διαφορά η 1 – ηΤο 2 είναι αμελητέα σε σύγκριση με την απόσταση από το κέντρο της Γης, μετά τη δύναμη της βαρύτητας φά m κατά την κίνηση του σώματος μπορεί να θεωρηθεί σταθερό και ίσο mg.

Εφόσον η μετατόπιση συμπίπτει ως προς την κατεύθυνση με το διάνυσμα της βαρύτητας, το έργο της βαρύτητας είναι

\ (~ A = F \ cdot s = m \ cdot g \ cdot (h_1 - h_2) \). (5)

Ας εξετάσουμε τώρα την κίνηση ενός σώματος κατά μήκος ενός κεκλιμένου επιπέδου. Όταν το σώμα κινείται προς τα κάτω σε κεκλιμένο επίπεδο (Εικ. 2), η δύναμη της βαρύτητας φά t = m ∙ gκάνω δουλειά

\ (~ A = m \ cdot g \ cdot s \ cdot \ cos \ άλφα = m \ cdot g \ cdot h \), (6)

όπου η- το ύψος του κεκλιμένου επιπέδου, μικρό- μέτρο μετατόπισης ίσο με το μήκος του κεκλιμένου επιπέδου.

Κίνηση σώματος από ένα σημείο Vακριβώς ΜΕκατά μήκος οποιασδήποτε τροχιάς (Εικ. 3) μπορεί να αναπαρασταθεί νοερά ως αποτελούμενη από μετατοπίσεις κατά μήκος τμημάτων κεκλιμένων επιπέδων με διαφορετικά ύψη η’, η'' Κλπ. Εργασία ΕΝΑβαρύτητα σε όλη τη διαδρομή από V v ΜΕισούται με το άθροισμα των έργων σε ξεχωριστά τμήματα του κομματιού:

\ (~ A = m \ cdot g \ cdot h "+ m \ cdot g \ cdot h" "+ \ ldots + m \ cdot g \ cdot h ^ n = m \ cdot g \ cdot (h" + h "" + \ ldots + h ^ n) = m \ cdot g \ cdot (h_1 - h_2) \), (7)

όπου η 1 και η 2 - ύψη ​​από την επιφάνεια της Γης, στα οποία βρίσκονται τα σημεία, αντίστοιχα Vκαι ΜΕ.

Η ισότητα (7) δείχνει ότι το έργο της δύναμης της βαρύτητας δεν εξαρτάται από την τροχιά του σώματος και είναι πάντα ίσο με το γινόμενο του συντελεστή της δύναμης της βαρύτητας από τη διαφορά ύψους στην αρχική και την τελική θέση.

Όταν κινούμαστε προς τα κάτω, το έργο της βαρύτητας είναι θετικό, όταν ανεβαίνουμε, είναι αρνητικό. Το έργο της βαρύτητας σε μια κλειστή διαδρομή είναι μηδέν.

Η ισότητα (7) μπορεί να αναπαρασταθεί ως εξής:

\ (~ A = - (m \ cdot g \ cdot h_2 - m \ cdot g \ cdot h_1) \). (οκτώ)

Το φυσικό μέγεθος που ισούται με το γινόμενο της μάζας του σώματος από το μέτρο επιτάχυνσης της βαρύτητας και το ύψος στο οποίο ανυψώνεται το σώμα πάνω από την επιφάνεια της γης ονομάζεται δυναμική ενέργειααλληλεπίδραση του σώματος και της Γης.

Το έργο της βαρύτητας όταν κινείται ένα σώμα με μάζα Μαπό σημείο που βρίσκεται σε ύψος η 2, σε σημείο που βρίσκεται σε ύψος η 1 από την επιφάνεια της Γης, κατά μήκος οποιασδήποτε τροχιάς ισούται με τη μεταβολή της δυνητικής ενέργειας αλληλεπίδρασης μεταξύ του σώματος και της Γης, που λαμβάνεται με το αντίθετο πρόσημο.

\ (~ A = - (E_ (p2) - E_ (p1)) \). (εννέα)

Η δυναμική ενέργεια υποδεικνύεται με το γράμμα μιΠ.

Η τιμή της δυναμικής ενέργειας ενός σώματος που υψώνεται πάνω από τη Γη εξαρτάται από την επιλογή του μηδενικού επιπέδου, δηλαδή το ύψος στο οποίο η δυναμική ενέργεια λαμβάνεται ως μηδέν. Συνήθως θεωρείται ότι η δυναμική ενέργεια ενός σώματος στην επιφάνεια της Γης είναι μηδέν.

Με αυτή την επιλογή του μηδενικού επιπέδου, η δυναμική ενέργεια μι p ενός σώματος σε ύψος ηπάνω από την επιφάνεια της γης, είναι ίσο με το γινόμενο της μάζας m του σώματος από το μέτρο της βαρυτικής επιτάχυνσης σολκαι απόσταση ηαπό την επιφάνεια της Γης:

\ (~ E_p = m \ cdot g \ cdot h \). (δέκα)

Η φυσική έννοια της δυνητικής ενέργειας αλληλεπίδρασης του σώματος με τη Γη

η δυναμική ενέργεια του σώματος, η οποία επηρεάζεται από τη δύναμη της βαρύτητας, είναι ίση με το έργο που επιτελεί η δύναμη της βαρύτητας όταν το σώμα κινείται στο μηδενικό επίπεδο.

Σε αντίθεση με την κινητική ενέργεια της μεταφορικής κίνησης, η οποία μπορεί να έχει μόνο θετικές τιμές, η δυναμική ενέργεια ενός σώματος μπορεί να είναι θετική και αρνητική. Μάζα σώματος Μσε υψόμετρο η, όπου η < η 0 (η 0 - μηδέν ύψος), έχει αρνητική δυναμική ενέργεια:

\ (~ E_p = -m \ cdot g \ cdot h \).

Δυνητική ενέργεια βαρυτικής αλληλεπίδρασης

Δυνητική ενέργεια βαρυτικής αλληλεπίδρασης συστήματος δύο υλικών σημείων με μάζες Μκαι Μσε μια απόσταση rτο ένα από το άλλο, ισούται με

\ (~ E_p = G \ cdot \ frac (M \ cdot m) (r) \). (έντεκα)

όπου σολΕίναι η σταθερά της βαρύτητας και το μηδέν της δυναμικής ενέργειας ( μι p = 0) υιοθετείται στο r = ∞.

Δυνητική ενέργεια βαρυτικής αλληλεπίδρασης σώματος με μάζα Μμε τη Γη όπου η- ύψος σώματος πάνω από την επιφάνεια της Γης, Μ e είναι η μάζα της Γης, R e είναι η ακτίνα της Γης και το μηδέν της δυναμικής ενέργειας επιλέγεται στο η = 0.

\ (~ E_e = G \ cdot \ frac (M_e \ cdot m \ cdot h) (R_e \ cdot (R_e + h)) \). (12)

Υπό την ίδια προϋπόθεση για την επιλογή της μηδενικής αναφοράς, τη δυναμική ενέργεια της βαρυτικής αλληλεπίδρασης ενός σώματος με τη μάζα Μμε τη Γη για χαμηλά ύψη η (η « Rε) ισούται

\ (~ E_p = m \ cdot g \ cdot h \),

όπου \ (~ g = G \ cdot \ frac (M_e) (R ^ 2_e) \) είναι το μέτρο της βαρυτικής επιτάχυνσης κοντά στην επιφάνεια της Γης.

Δυνητική ενέργεια ενός ελαστικά παραμορφωμένου σώματος

Ας υπολογίσουμε το έργο που κάνει η ελαστική δύναμη όταν η παραμόρφωση (επιμήκυνση) του ελατηρίου αλλάζει από κάποια αρχική τιμή Χ 1 έως την τελική τιμή Χ 2 (Εικ. 4, β, γ).

Η ελαστική δύναμη αλλάζει καθώς το ελατήριο παραμορφώνεται. Για να βρείτε το έργο της ελαστικής δύναμης, μπορείτε να πάρετε τη μέση τιμή του συντελεστή της δύναμης (καθώς η ελαστική δύναμη εξαρτάται γραμμικά από Χ) και πολλαπλασιάζουμε με το συντελεστή μετατόπισης:

\ (~ A = F_ (upr-cp) \ cdot (x_1 - x_2) \), (13)

όπου \ (~ F_ (upr-cp) = k \ cdot \ frac (x_1 - x_2) (2) \). Από εδώ

\ (~ A = k \ cdot \ frac (x_1 - x_2) (2) \ cdot (x_1 - x_2) = k \ cdot \ frac (x ^ 2_1 - x ^ 2_2) (2) \) ή \ (~ A = - \ αριστερά (\ frac (k \ cdot x ^ 2_2) (2) - \ frac (k \ cdot x ^ 2_1) (2) \ δεξιά) \). (δεκατέσσερα)

Φυσικό μέγεθος ίσο με το μισό γινόμενο της ακαμψίας ενός σώματος με το τετράγωνο της παραμόρφωσής του ονομάζεται δυναμική ενέργειαένα ελαστικά παραμορφωμένο σώμα:

\ (~ E_p = \ frac (k \ cdot x ^ 2) (2) \). (15)

Από τους τύπους (14) και (15) προκύπτει ότι το έργο της ελαστικής δύναμης είναι ίσο με τη μεταβολή της δυναμικής ενέργειας ενός ελαστικά παραμορφωμένου σώματος, που λαμβάνεται με το αντίθετο πρόσημο:

\ (~ A = - (E_ (p2) - E_ (p1)) \). (16)

Αν Χ 2 = 0 και Χ 1 = NS, τότε, όπως φαίνεται από τους τύπους (14) και (15),

\ (~ E_p = A \).

Η φυσική έννοια της δυναμικής ενέργειας ενός παραμορφωμένου σώματος

η δυναμική ενέργεια ενός ελαστικά παραμορφωμένου σώματος είναι ίση με το έργο που εκτελείται από την ελαστική δύναμη κατά τη μετάβαση του σώματος σε μια κατάσταση στην οποία η παραμόρφωση είναι μηδέν.

Η δυναμική ενέργεια χαρακτηρίζει τα αλληλεπιδρώντα σώματα και η κινητική ενέργεια τα κινούμενα σώματα. Τόσο το δυναμικό όσο και η κινητική ενέργεια αλλάζουν μόνο ως αποτέλεσμα μιας τέτοιας αλληλεπίδρασης σωμάτων, κατά την οποία οι δυνάμεις που δρουν στα σώματα εκτελούν έργο διαφορετικό από το μηδέν. Ας εξετάσουμε το ζήτημα των ενεργειακών μεταβολών κατά τις αλληλεπιδράσεις των σωμάτων που σχηματίζουν ένα κλειστό σύστημα.

Κλειστό σύστημαΕίναι ένα σύστημα που δεν επηρεάζεται από εξωτερικές δυνάμεις ή η δράση αυτών των δυνάμεων αντισταθμίζεται... Εάν πολλά σώματα αλληλεπιδρούν μεταξύ τους μόνο με βαρυτικές δυνάμεις και ελαστικές δυνάμεις και δεν ασκούνται εξωτερικές δυνάμεις πάνω τους, τότε για οποιεσδήποτε αλληλεπιδράσεις σωμάτων, το έργο των ελαστικών δυνάμεων ή των βαρυτικών δυνάμεων είναι ίσο με τη μεταβολή της δυναμικής ενέργειας των σωμάτων. λαμβάνονται με το αντίθετο πρόσημο:

\ (~ A = - (E_ (p2) - E_ (p1)) \). (17)

Σύμφωνα με το θεώρημα της κινητικής ενέργειας, το έργο των ίδιων δυνάμεων είναι ίσο με τη μεταβολή της κινητικής ενέργειας:

\ (~ A = E_ (k2) - E_ (k1) \). (δεκαοχτώ)

Από μια σύγκριση των ισοτήτων (17) και (18), μπορεί να φανεί ότι η μεταβολή της κινητικής ενέργειας των σωμάτων σε ένα κλειστό σύστημα είναι ίση σε απόλυτη τιμή με τη μεταβολή της δυναμικής ενέργειας του συστήματος των σωμάτων και είναι αντίθετη. σε αυτό σε ένδειξη:

\ (~ E_ (k2) - E_ (k1) = - (E_ (p2) - E_ (p1)) \) ή \ (~ E_ (k1) + E_ (p1) = E_ (k2) + E_ (p2) \). (19)

Ο νόμος εξοικονόμησης ενέργειας στις μηχανικές διεργασίες:

το άθροισμα της κινητικής και της δυναμικής ενέργειας των σωμάτων που αποτελούν ένα κλειστό σύστημα και αλληλεπιδρούν μεταξύ τους με τις δυνάμεις της βαρύτητας και τις δυνάμεις της ελαστικότητας, παραμένει σταθερό.

Το άθροισμα της κινητικής και της δυναμικής ενέργειας των σωμάτων λέγεται πλήρης μηχανική ενέργεια.

Ας δώσουμε απλούστερη εμπειρία... Ας ρίξουμε μια ατσάλινη μπάλα. Έχοντας ενημερώσει την αρχική ταχύτητα υ εκκίνησης, θα του δώσουμε κινητική ενέργεια, λόγω της οποίας θα αρχίσει να ανεβαίνει προς τα πάνω. Η δράση της βαρύτητας οδηγεί σε μείωση της ταχύτητας της μπάλας και ως εκ τούτου της κινητικής της ενέργειας. Αλλά η μπάλα ανεβαίνει όλο και πιο ψηλά και αποκτά όλο και περισσότερη δυναμική ενέργεια ( μι p = m ∙ g ∙ h). Έτσι, η κινητική ενέργεια δεν εξαφανίζεται χωρίς ίχνος, αλλά μετατρέπεται σε δυναμική ενέργεια.

Τη στιγμή που θα φτάσετε στο κορυφαίο σημείο της τροχιάς ( υ = 0) η μπάλα στερείται εντελώς κινητικής ενέργειας ( μι k = 0), αλλά ταυτόχρονα η δυναμική του ενέργεια γίνεται μέγιστη. Στη συνέχεια η μπάλα αλλάζει την κατεύθυνση της κίνησής της και κινείται προς τα κάτω με αυξανόμενη ταχύτητα. Τώρα λαμβάνει χώρα η αντίστροφη μετατροπή της δυναμικής ενέργειας σε κινητική.

Ο νόμος της διατήρησης της ενέργειας αποκαλύπτει φυσική έννοιαέννοιες εργασία:

το έργο των βαρυτικών δυνάμεων και των ελαστικών δυνάμεων, αφενός, ισούται με αύξηση της κινητικής ενέργειας και, αφετέρου, με μείωση της δυναμικής ενέργειας των σωμάτων. Κατά συνέπεια, το έργο ισούται με την ενέργεια που μετατρέπεται από τον έναν τύπο στον άλλο.

Νόμος για την μεταβολή της μηχανικής ενέργειας

Εάν το σύστημα των σωμάτων που αλληλεπιδρούν δεν είναι κλειστό, τότε η μηχανική του ενέργεια δεν διατηρείται. Η αλλαγή στη μηχανική ενέργεια ενός τέτοιου συστήματος είναι ίση με το έργο των εξωτερικών δυνάμεων:

\ (~ A_ (vn) = \ Delta E = E - E_0 \). (είκοσι)

όπου μικαι μι 0 - συνολικές μηχανικές ενέργειες του συστήματος στην τελική και αρχική κατάσταση, αντίστοιχα.

Ένα παράδειγμα τέτοιου συστήματος είναι ένα σύστημα στο οποίο οι μη δυνητικές δυνάμεις δρουν μαζί με τις δυνάμει δυνάμεις. Οι μη δυνητικές δυνάμεις περιλαμβάνουν δυνάμεις τριβής. Στις περισσότερες περιπτώσεις, όταν η γωνία μεταξύ της δύναμης τριβής φά rσώμα είναι π ακτίνιο, το έργο της δύναμης τριβής είναι αρνητικό και ίσο με

\ (~ A_ (tr) = -F_ (tr) \ cdot s_ (12) \),

όπου μικρό 12 - διαδρομή σώματος μεταξύ των σημείων 1 και 2.

Οι δυνάμεις τριβής κατά την κίνηση του συστήματος μειώνουν την κινητική του ενέργεια. Ως αποτέλεσμα αυτού, η μηχανική ενέργεια ενός κλειστού μη συντηρητικού συστήματος μειώνεται πάντα, μετατρέποντας σε ενέργεια μη μηχανικών μορφών κίνησης.

Για παράδειγμα, ένα αυτοκίνητο που κινείται κατά μήκος ενός οριζόντιου τμήματος του δρόμου, αφού σβήσει τον κινητήρα, διανύει μια ορισμένη απόσταση και σταματά υπό την επίδραση των δυνάμεων τριβής. Η κινητική ενέργεια της μεταφορικής κίνησης του οχήματος έγινε μηδέν και η δυναμική ενέργεια δεν αυξήθηκε. Κατά το φρενάρισμα του οχήματος προέκυψε θέρμανση των τακακιών, των ελαστικών του οχήματος και της ασφάλτου. Κατά συνέπεια, ως αποτέλεσμα της δράσης των δυνάμεων τριβής, η κινητική ενέργεια του αυτοκινήτου δεν εξαφανίστηκε, αλλά μετατράπηκε στην εσωτερική ενέργεια της θερμικής κίνησης των μορίων.

Ο νόμος της διατήρησης και του μετασχηματισμού της ενέργειας

σε οποιεσδήποτε φυσικές αλληλεπιδράσεις, η ενέργεια μετατρέπεται από τη μια μορφή στην άλλη.

Μερικές φορές η γωνία μεταξύ της δύναμης τριβής φά tr και στοιχειώδης μετατόπιση Δ rείναι μηδέν και το έργο της δύναμης τριβής είναι θετικό:

\ (~ A_ (tr) = F_ (tr) \ cdot s_ (12) \),

Παράδειγμα 1... Άσε, εξωτερική δύναμη φάενεργεί στο μπαρ Vπου μπορεί να γλιστρήσει στο καλάθι ρε(εικ. 5). Εάν το φορείο κινείται προς τα δεξιά, τότε το έργο της δύναμης τριβής ολίσθησης φάΤο tr2 που ενεργεί στο τρόλεϊ από την πλευρά της ράβδου είναι θετικό:

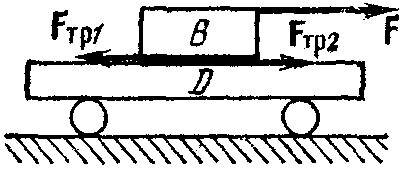
Παράδειγμα 2... Όταν ο τροχός κυλά, η δύναμη τριβής κύλισής του κατευθύνεται κατά μήκος της κίνησης, καθώς το σημείο επαφής του τροχού με την οριζόντια επιφάνεια κινείται προς την αντίθετη κατεύθυνση από την κατεύθυνση της κίνησης του τροχού και το έργο της δύναμης τριβής είναι θετικό (Εικ. 6):

Λογοτεχνία

1. O.F. Kabardin Φυσική: Κωδ. Υλικά: Σχολικό βιβλίο. εγχειρίδιο για μαθητές. - Μ .: Εκπαίδευση, 1991 .-- 367 σελ.
2. Kikoin I.K., Kikoin A.K. Φυσική: Σχολικό βιβλίο. για 9 cl. Τετάρτη shk. - M .: Pro-sveshenie, 1992 .-- 191 p.
3. Βιβλίο φυσικής Δημοτικού: Σχολικό βιβλίο. επίδομα. Σε 3 τόμους / Εκδ. Ο Γ.Σ. Landsberg: τ. 1. Μηχανική. Θερμότητα. Μοριακή φυσική. - M .: Fizmatlit, 2004 .-- 608 p.
4. Yavorskiy B.M., Seleznev Yu.A. Ένας οδηγός αναφοράς για τη φυσική για τους υποψήφιους πανεπιστημίου και την αυτοεκπαίδευση. - M .: Nauka, 1983 .-- 383 p.